Grand Prix of Europe

→ Обратите внимание

До соревнования
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
5 дней
Зарегистрироваться »

*есть доп. регистрация

→ Лидеры (рейтинг)

№	Пользователь	Рейтинг
1	tourist	3993
2	jiangly	3743
3	orzdevinwang	3707
4	Radewoosh	3627
5	jqdai0815	3620
6	Benq	3564
7	Kevin114514	3443
8	ksun48	3434
9	Rewinding	3397
10	Um_nik	3396

Страны | Города | Организации

Всё →

→ Лидеры (вклад)

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	156
8	TheScrasse	154
9	Dominater069	153
10	nor	152

Всё →

→ Найти пользователя

→ Прямой эфир

Детальнее →

Блог пользователя Tima

Grand Prix of Europe

Автор Tima, история, 7 лет назад, По-английски

Let's discuss problems. How to solve C,K?

Tima
7 лет назад
24

Комментарии (24)

Написать комментарий?

eddy1021

7 лет назад, # |

+18

How to solve I?

→ Ответить

markysha

7 лет назад, # |

G, L?

→ Ответить

pitfall

7 лет назад, # ^ |

+20

G: You can use dijkstra-like approach: start from vertex n with expected(n)=0. Relaxation will looks like: for vertex V we will use edges corresponding only to fixed(by dijkstra algo) vertexes.

→ Ответить

pitfall

7 лет назад, # ^ |

+10

L: you can find answer for squares with/without rotation by 2D scanline (for rotated squares you need to make transition to diagonal coordinate system), and then you need to merge both answers by rotating second. Implementation little bit tricky and unfortunately we didn't have enough time to debug it, but I think that it is correct idea.

→ Ответить

markysha

7 лет назад, # ^ |

We thought about this solution but also didn't write it.
Finally we wrote O(n·1500) solution and it got TL.
I wonder if there exists a bit easier solution.

→ Ответить

MrDindows

7 лет назад, # ^ |

I solved it with prefix-sums. For rotated squares I just built 4 arrays, for each triangle type that is a half of rectangle cell, and used diagonal-2d prefix sums without explicit rotation. Idk if it is easier, but it uses single coordinate system. https://ideone.com/PXu3Np

→ Ответить

kalinov

7 лет назад, # ^ |

Here's an implementation of the in-memory painting algorithm described in the slides. It's surprisingly simple: https://pastebin.com/NxJt4C9k

a[x][y] = k tells us we need to paint the type-A square of size k: (x, y) — (x + k, y + k).

b[x][y] = k tells us we need to paint the type-B square of size k: (x, y) — (x + k, y).

You can figure out the painted area for each unit square (x, y) — (x + 1, y + 1) by looking at the values at a[x][y] and in the neighborhood of b[x][y].

→ Ответить

Djok216

7 лет назад, # |

How to solve J?

→ Ответить

markysha

7 лет назад, # ^ |

← Rev. 2 →

Let's try every possible k. If we delete k edges there will be k + 1 components, each of size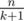 $\text{[math]}$ . There are about 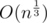$\text{[math]}$ possible k.
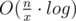Now we have another task. Determine if we can split tree into parts, each of some size x. Let's root our tree and calculate pr[v] — nearest vertex on path from v to root, and sz[v] — size of subtree with root = v. Let's notice that if we delete edge (pr[v], v) then x must be a divisor of sz[v]. So let's iterate over all v that satisfy this condition in increasing order of sz[v]. And now when we are in vertex v, we want to know how many edges we have already deleted in subtree with root = v. If we deleted y edges then sz[v] must be equal to (y + 1)·x, then we can delete edge (pr[v], v). It can be done in log(n) with fenwick tree and top-sort.
So for fixed x it works in $\text{[math]}$ .

→ Ответить

rmn

7 лет назад, # ^ |

My teammate had an interesting simple solution to this problem.

Run DFS from vertex 1 to calculate the number of vertices in each subtree. Then to check if the tree can be divided into components with K vertices in each component:

N must be divisble by K
the number of subtrees whose size is divisible by K, must be equal to N/K

→ Ответить

I_Love_Tina

7 лет назад, # ^ |

+19

There is a harder problem which contains the same idea.

Short statement: A tree T₁ has a divisor T₂ if we can delete some edges from tree T₁ so that the remaining trees in the forest are isomorphic to T₂. Given a tree find how many divisors it has.

→ Ответить

pavel.savchenkov

7 лет назад, # |

+40

We can consider knobs with single maximal shift (otherwise every shift would be maximal, so we can skip this knob). So we have x_r for each 1 ≤ r ≤ n, at each step we can add some value to some segment. Let's do it in another way: add v to y_l, add - v to y_r + 1. Then calculate prefix sums of y, this new array must be equal to x. From this we can find all values of y: y_r = x_r - x_r - 1.

Now the answer depends only on amount of each value modulo 7. Our operations are: add v to some value, add - v to another value or just add v to some value. The goal is to get all zeros. If we draw an edge between two values iff they were in one operation, then each connected component will have zero sum modulo 7. But each component of values with zero sum can be eliminated in component_size-1 steps. So we want to find maximal number of disjoints components with zero sum. After eliminating all z with - z (modulo 7), we are left with ≤ 3 values, so we can handle them with O(n³) dp.

→ Ответить

kalinov

7 лет назад, # |

+20

The slides from the solution presentation held onsite may help to get high-level ideas: goo.gl/bwJpds

Some problems have multiple ways to approach them, so keep the discussion going!

→ Ответить

Kostroma

7 лет назад, # ^ |

+10

I have a question about the solution of I described in the editorial: why we can consider only segments expanded to the right from [mid;mid + 1] and to the left of it? Maybe we must improve the answer by the intersection of the smallest "left" and "right" segments containing the query, but not the smallest of them?

→ Ответить

pavel.savchenkov

7 лет назад, # ^ |

← Rev. 2 →

+10

Expand operation can be implemented as follows:

Seg expand(int l, int r) {
        mn = get_min_value(l, r);
	mx = get_max_value(l, r);
	min_pos = min{pos[mn], ..., pos[mx]};
	max_pos = max{pos[mn], ..., pos[mx]};
	assert(min_pos <= l && r <= max_pos);
	return Seg{min_pos, max_pos};
}

In slow solution we can call expand(l, r) until we get good interval, call this operation getAnswer(l, r). Another observation: if l ≤ l' ≤ r' ≤ r, then segment getAnswer(l, r) will contain segment getAnswer(l', r'). So the answer for [l, r] must contain answers for any l ≤ l' ≤ r' ≤ r. ~~Even more: as far as I understand, answer for [l, r] equal to union of answers for any set of segments with union of this set is exactly [l, r].~~

UPD: the last statement obviously not true, we can take all segments with length = 1; maybe we must make this set of segments connected (edge between segments iff their intersection is not empty). Anyway, this is true for {[l, mid + 1], [mid, r]}.

→ Ответить

kalinov

7 лет назад, # ^ |

+30

Yes, I had it wrong in the presentation. Thanks for pointing it out!

I believe it should be:
1) Within the left intervals find the smallest one that covers a.
2) Within the right intervals find the smallest one that covers b.
3) The union of 1) and 2) is the smallest interval that covers the entire [a, b] range.

→ Ответить

Kostroma

7 лет назад, # ^ |

+10

Our solution of I that passed is as follows: for each i we take values i and i + 1 and find what interval they generate. After this step for each query [x;y] we find min and max on the segment and unite intervals for all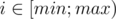 $\text{[math]}$ .

How we do the first step: take minimal segment containing i and i + 1 and start to expand it step by step using sparse table (take min and max on the segment, take min and max on corresponding segment of the inverse permutation and so on). The only hack we use is when i - 1 got into current segment, we relax the borders of the current segment by the interval found for i - 1 and i.

We don't know whether it works on all permutation in less than O(n²) and don't have an idea of counter-test, so I'll appreciate any help in understanding the complexity of this solution :)

→ Ответить

MrDindows

7 лет назад, # ^ |

+10

The only hack we use is when i - 1 got into current segment

Do you look only at (i-1, i), or at each less pair? If only i-1, I think the following test will be counter-test:
1 6 2 3 9 4 5 12 7 8 15 10 11 18 13 14 21 16 17 24...

→ Ответить

Kostroma

7 лет назад, # ^ |

In this test almost all pairs i and i + 1 that are not consecutive in the array have i - 1 between them, so we relax them fast, don't we?

→ Ответить

MrDindows

7 лет назад, # ^ |

← Rev. 2 →

+10

Pair 5-6 have 4 between them, but there is nothing to relax, because 4 and 5 are near. Same for 8-9, 11-12 etc

→ Ответить

Kostroma

7 лет назад, # ^ |

+10

Thank you, it works 17s on this test =)

→ Ответить

wannared

7 лет назад, # |

Sorry If this is stupid question. But Can you please mention some details about these contests in blog. I have seen similar "Grand Pix" blogs before as well.. Where can I find problems of these contests?

→ Ответить

rmn

7 лет назад, # ^ |

What is Grand Prix?

This particular round was based on problems from CERC 2017.

→ Ответить

rsFalse

7 лет назад, # |

Problem A was difficult to implement, used much lines. It was the problem mostly about proper sorting. Later upsolved it more compactly.

→ Ответить

Соревнования по программированию 2.0

Время на сервере: 25.11.2024 11:08:49 (i1).

Десктопная версия, переключиться на мобильную.

При поддержке