Date and time : https://www.timeanddate.com/worldclock/fixedtime.html?msg=SRM%20725&iso=20171209T1700&ah=2&am=0
Edit: Problem Analysis (Except Div1 1000 ) by Morphy : https://aleigorithms.wordpress.com/2017/12/10/srm-725/
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Date and time : https://www.timeanddate.com/worldclock/fixedtime.html?msg=SRM%20725&iso=20171209T1700&ah=2&am=0
Edit: Problem Analysis (Except Div1 1000 ) by Morphy : https://aleigorithms.wordpress.com/2017/12/10/srm-725/
| Название |
|---|



REMINDER: The contest starts in 40 minutes.
Let's register and participate! Don't forget!
Why do i have to find it 1 hour after registration began? If they want people to participate in their round they can allow admin to announce round on cf instead of putting the 5$ prize.
I can't compile in arena :(
You can not compile in a contest that is not active
Same here
I think this is going to be unrated.
Same for me, thank topcoder for a great experience. Hope the round will be unrated.
Same here. I hope this is going to be unrated.
I faced on the same issue :(
I coded solution for 1000-point problem before finish, and couldn't compile/submit it until the end of a contest. Too bad :(
How to solve div. 1 hard?
I think I know how to reduce it to min-cut problem, although I didn't manage to fix all problems by the end of the contest. Anyway, here it goes:
For every node in the original graph we'll create its own chain of nodes 0...100. Let's call these nodes nn[v][i] where v is the recipe from the original graph. Node i in this chain will be responsible for answering the question "is it true that we finish this recipe preparation at time X <= i?" (I'll call this predicate p[i]). We can add edges from i to i-1 of infinite capacity to make sure that if p[i] is true, then p[i + 1] is also true. Also, we can add an edge of infinite capacity from the source S to all nodes i < prep_time[v] and also add an edge from node 100 in the chain to T of infinite capacity.
To satisfy topological sorting constraints, for each dependency (v, u) we can add edges of infinite capacity between nn[v][i] and nn[u][j] where (j - i = preptime[v]).
Now, min-cut in the described graph will give us some ordering which would satisfy the correctness constraints, although it's not going to minimize the staleness.
Let's take a look at a pair of nodes (v, u) with dependency v->u. Let fin[i] be the time where we finish preparing node i, st[i] be the start of preparation which is equal to fin[i] - preptime[i]. Then, for (v, u) we'll need to add (st[v] - fin[u])2 to the total staleness. This can be expressed in the following form: (st[v] - fin[u])2 = st[v]2 + fin[u]2 - 2·st[v]·fin[u]. Note that st[v]2 and fin[u]2 don't depend on the pair (v,u) so they can be easily incorporated into our graph if we add edges between nn[v][i] and nn[v][i + 1] of corresponding weights, multiplied by in-degree or out-degree.
Now, let's add edges of capacity 2 between all pairs of nodes nn[v][i] and nn[u][j] for each dependency (v, u). Let's assume we've found the min-cut and let's only look at the edges that intersect it. If node v is finished at time i, then there'll be a cut between nn[v][i] and nn[v][i + 1]. Similarly, let's assume node u is finished at time j so there's a cut between nn[u][j] and nn[u][j + 1]. Then, all edges from nn[v][i'] (i' ≤ i) to nn[u][j'] (j' ≥ j) will belong to the cut, which means we'll add smth like 2·fin[v]·(100 - fin[u]) = 200·fin[v] - 2·fin[v]·fin[u] to the overall answer which is almost what we need. We'd still need to subtract 200·fin[v] from the answer, and also we'd need to convert 2·fin[v]·fin[u] into 2·fin[v]·st[u] = 2·fin[v]·fin[u] - 2·fin[v]·preptime[u], however that can be done quite easily by adding carefully chosen edges.
Now, if we find a min-cut in this graph, it'll give us the minimum total staleness.
I have a solution in the practice room that works on roughly these principles, and which passes system tests. I didn't use the infinite edges from i to i-1; instead I used a large finite capacity on the edges i to i+1, which ensures that no more than one cut is made in any chain. I also adjusted the capacities of the dependency edges such that the min-cut is just the answer plus a constant to compensate for the cut along each change.
I guess it’s just a question of whether your left part of the cut (the one with the source) contains an answer “YES” (i.e. nodes from these chains whose constraints are satisfied) or “NO”. For me it’s the latter, I guess for you it’s the former.
This time, the answer to the most asked question on CodeForces is "No". It's already been announced that it is NOT rated.
How to solve Div2 500-point problem?
You can pretend all tasks are instant by subtracting time[i] from start[i+1], then binary search the answer using greedy. Which turns out to be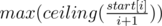
Div 2 500 can be solved with a binary search over the answer. You need to guess the answer value and check if all the task can be done using this time gap. If it is possible then you need to decrease your search range otherwise you need to increase your search range.
BTW, there is no need to implement binary search. The limit is low, so linear search would do. Complexity will be rangesize(10^6) * sizeofarray(50).
They really need to put instructions on how to avoid using the horrible topcoder webapp... I spent half an hour googling to setup the java web start with greed plugin. But I think most first-time users won't bother
Today's Div2 250 problem was some kind of "obvious" brute-force solution so I thought that SRM Div1 250 problem can be better (because problem making cost (time) is less than SRM Div1 500 or 1000).
From Arena messages:
That's something new. Does "not being able" mean the rating procedure somehow broke beyond repair?
It means the round can't be rated because of failure with compiling solutions in the second half of it.
Thanks for the information! I had to leave after submitting the second problem, so didn't experience the issue.
Div2 1000 any one please? How to approach it?
If you can't give us rating, at least give us practice rooms ;_;
I crawled out of my hiding to participate, and it's unrated. uh oh.
p.s. screw rating, I want it at least appear in some list
Problem analysis of all except div1 1000: https://aleigorithms.wordpress.com/2017/12/10/srm-725/
Great blog! Added to main post so people can find it easier.
Since I didn't see it mentioned here, I'll add a proof of existence for Div1 250 (my actual solution was to hit it with bipartite matching, but this existence proof also leads to a constructive algorithm).
Consider a specific maximum set of non-attacking rooks, of size M. Colour the board so that the columns containing those rooks are red, the rows containing those rooks are blue, and cells that qualify to be both red and blue are purple. Consider a single chosen rook. If it attacks non-purple rooks in both its row and column, it could be removed and replaced by those two rooks, giving a larger matching. Thus, it can attack at most 8-M red/blue rooks. Furthermore, summing this count over the chosen rooks counts each red/blue rook exactly once, so there are at most M(8-M) such rooks. Cells without colour also cannot contain rooks (otherwise they could be trivially added to the maximum set) and there are at most M^2 purple rooks (one per cell), so there there are at most M^2 + M(8-M) = 8M rooks in total. Since we know there have to be least 33, M >= 5.
Or just group them by (x+y)%8.
Ah, that's nice! I was hoping to find some simple pigeon-hole solution but didn't spot this approach.
Besides it's not rated, does anyone know where to find the results of the system tests? At least I want to know if my 250 passed the system tests