Can we find matrix modular inverse as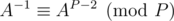
?
Related question/answer
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
38:33:37
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
38:33:37
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 03:01:23 (k2).
Десктопная версия, переключиться на мобильную.
При поддержке
clearly no?
A= 2*I where I is the identity
P = 5
A^3 = (2*I)^3 = 8*I, while A^-1 = (0.5*I).
right, sorry my bad for giving such a poor example as i wanted to ease calculation.
For diagonal matrices it's also true. For diagonalisable invertible matrices, it looks OK, surprisingly. For matrices not diagonalisable, it is in general false. See e.g.
To the power a it is
therefore the inverse is given for the power a=p-1 and not p-2 (yeah it's close, but...)
For arbitrary matrices it's false. For example,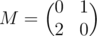
. Mp - 1 = 2(p - 1) / 2E. If 2 isn't a square modulo p, Mp - 1 ≠ E.
Also you can use Lagrange's theorem for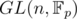
group. The order of this group is (pn - 1)(pn - p)... (pn - pn - 1). For n = 2 we get A(p2 - 1)(p2 - p) = E. Doesn't look like the best estimation, though.
The fact that the right hand side always exists and the left hand side doesn't have to exist hints that it shouldn't be so.
Look up the Jordan form. Not only does it tell you when it's possible to use FLT, it basically gives you a formula for matrix powers (in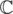
, not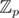 
). Of course, computing the Jordan form is itself difficult and you're better off just using fast exponentiation.