Hello Codeforces, on the 1st stage of the lastest Polish Olympiad in Informatics, appeared a problem which I could not get full score for. I would be very thankful, could somebody provide me with an efficient solution.
Self-translated statement: (Różnorodność, in Polish https://szkopul.edu.pl/problemset/problem/eHGwrk9xShVF-z_2f7K4Yyb_/statement/)
You're given a 2d array of integers. Subarrays of this array, of size KxK we will call it's K-fragments. "Diversity" of a K-fragment we will call the number of different elements it contains. You are to count the max diversity of a K-fragment, out of all possible and the sum of diversities from all K-fragments of the array.
Input: First line contains 3 integers m,n,K denoting the array size (mxn) and size of fragments (KxK). m,n,K <= 3000
The next m lines has n integers being the successive numbers of the array. The numbers are in interval [1,100000].
Example:
For input: the right output is:
3 5 2 4 20
1 5 3 3 3
4 1 3 3 4
4 2 4 4 3
The memory limit is 512MB, time limit 15 seconds.
I made a solution, which traversed through every K-fragment, by erasing the first K element column of the previous fragment, and including new column of K elements.
For that I got only 64 points from a total of 100.










Identify each K-fragment with it's top-left corner. For a fixed cell, the corners of the K-fragments containing it form a k by k square.(If we allow corners that lead to a K-fragment that exceedes the array.)
For each number in the array, the area of corners containing that number is the union of these squares. This area can be decomposed into disjoint rectangles by sweepline with a set containing active intervalls and their creation time.
For each such rectangle, do an update in a 2D prefix sum. In the end, the prefix sum contains the number of different numbers for each K-Fragment, so just take the sum and maximum.
The total runtime is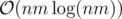 .
.
Isn't that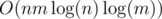 ?
?
I think you should calculate matrix A with A[i][j] being the answer to fragment with bottom left corner (i, j). Now when you have a fragment you will mark for every different value in this fragment only the one with the smallest row, and in case of equality with the smallest column. The diversity of the fragment is the sum of marked cells. Now for every cell, you will count in how many fragments it is marked, but the bottom left corners of these fragments form a submatrix, for example in case of (3, 3) the submatrix has corners (1, 2) and (3, 3). I hope it is clear now how to find the answer.
The complexity is O(n × m) if I'm not mistaken.
Maybe I don't understand, but I don't see how you can find the answer clearly.
Suppose the initial matrix is R. Now I say that the first occurrence of value v in matrix T is the smallest pair (i, j) with T[i][j] = v. Now for each cell (i, j) I would like to find the submatrices where the first occurrence of value R[i][j] is (i, j). Clearly if such a submatrix have bottom left corner (x, y), then we have that 1 ≤ x ≤ i and 1 ≤ y ≤ j because this submatrix must contain cell (i, j). Because (i, j) is the first occurence, let cell (i1, j1) be the largest cell with 1 ≤ i1 < i, R[i1][j1] = R[i][j] and (i2, j2) be the largest cell with 1 ≤ j2 < j, R[i2][j2] = R[i][j]. Now we see the satisfying submstrices are only those with (i2 < x ≤ i and j1 < y ≤ j) or (i2 < x ≤ i and 1 ≤ y ≤ j) or (1 ≤ x ≤ i and j2 < y ≤ j).
Hope it's clear now. Please correct me if something is wrong.
Where can I find the other problems from this contest?
Here: www.szkopul.edu.pl/portal/problemset/oi/25 But only in Polish for now.
When will the translations of recent POI problems be available? The latest ones I could access were from around 2013.
Frankly, I don't know. :(