Hi! I have been trying the following problem for some time now and haven't been able to come up with a solution better than O(N^2).
Given an array A with N integers, define maxi, j to be the maximum value in A[i..j] and mini, j to be the minimum value in A[i..j]. A[i..j] denotes the subarray starting from index i and ending at j. Compute the following sum:
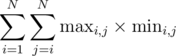
Please let me know if this problem is available on some OJ.











Your problem kinda looks like this: https://csacademy.com/contest/round-35/task/min-max-sum/statement/
I guess the editorial solution should work with my problem. I have to sum Vi without the pi - 1 factor.
Thanks for the help!
there is 1 more solution with divide and conquer, for a range [l, r], fix mid = (l + r) / 2 and find sum of max(i,j) * min(i, j) for ranges (i, j) that contain mid in O(r — l + 1)
then u remove mid and solve for (l, mid — 1) and (mid + 1, r)
I did consider this way of thinking but I do not see how to compute the answer for ranges containing mid in linear time.
range [i, j] containing mid will be a suffix [i, mid] and prefix [mid + 1, j]
now you have to precalculate all suffix maxima , minima and same for prefix
And you have 4 cases: minimum is in suffix, but maximum is in prefix
or vice versa
Or Both are in prefix, or Both are in suffix
you need to treat all 4 cases separately
note that suffix maxima is increasing, suffix minima is decreasing, prefix maxima is increasing, prefix minima is decreasing
Now think how you can solve this with 2 pointers approach
I think that it can be solved using divide and conguer. The complexity will be O(nlogn)
Another very similar problem is Norma from COCI 2014/15.
You can submit it here.
How to solve it?