Tutorial is loading...
Code (C++ version)
Tutorial is loading...
Code (C++ version)
Code (Python version)
Tutorial is loading...
Code (C++ version)
Code (Python version)
Tutorial is loading...
Code (C++ version)
Tutorial is loading...
Code (C++ version)
Tutorial is loading...
Code (My stupid solution: C++ version)
Code (demon1999's fast solution: C++11 version)
UPD1: Note that the editorial of problem E is modified with some correction. Sorry for that inconvenience.
UPD2: The editorial is complete now. Hope you find it useful. :P
UPD3: It's seems that all bonus questions can be found in the comments. :) Don't hesitate to give them an upvote. :P
UPD4: The editorial is updated.











For B, instead of going for every number, we can move at intervals of 9 probably?
yes you can but you have to go for brute for near every multiple of 100.
http://mirror.codeforces.com/contest/919/submission/34774559
Its just simple checking.... seems good to go.
My solution for B question has complexity O( k * (log(2 * 10^7)[base 9]) * 10 ).
Source code: link
Is this the optimized one that you are talking about @jinlifu1999
For B, Bonus1: Iterate from 1 and for every number n whose sum of digits is less than 10, answer is concatenation of n and 10 - sum(n). This is 10 times faster than mentioned brute-force.
Submission
I also thought of this approach but this is not efficient for solving Bonus2. Do you have any idea, how to solve for Bonus2?
Binary Search + DP. We binary search over the answer and for a fixed ans we check how many numbers smaller or equal to this has digit-sum 10 using DP. And whether that is grater, equal or smaller than given k.
My Solution. We would have to use Bigint and larger constraints for the DP for it to work for k upto 10^18.
Actually, you don't need to use binary search. http://mirror.codeforces.com/contest/919/submission/34803226 The complexity is O(number of digits in answer * 10) for computing the table ignoring the need to use BigInt.
Could you please explain your idea a bit. I saw your code but didn't quiet understand what you were doing.
dp[i][s] = number of numbers with i digits (leading 0-s counts) and sum of digits s
Every possible number [i][s] is a path from [i][s] to [0][0]. So you start looking at some number of digits and the sum you want. Try putting a 0 in the last position. dp[i — 1][s — 0] is the number of such numbers. If that's lesser than the n that you are looking for, you know that the number you want has some number greater than 0 in this position, so you exclude the numbers that have the same prefix and 0 in this position (n -= dp[i — 1][s — 0]) and try it for 1. Keep on trying for all the next digits 0 <= j <= 9 until n <= dp[i — 1][s — j]. Now you know that the number you are looking for has digit j in this position and can do the same process for i — 1 until getting to i == 0.
Awesome idea!! You must have a deep understanding in dp. The way you formulate dp[i][j] really surprised me (dp in dp)! Learned a lot from your word and code.
But I think
n >= dp[i — 1][s — j]should ben <= dp[i — 1][s — j]. Is that right?That's right! My mistake.
Thanks for the detailed explanation. As a follow-up question: why do we need to exclude the numbers that have the same prefix and digit j in position i (n -= dp[i-1][s-j])?
In this way to code dp on digits, you fix a prefix and look for the next digit. If you are looking for the n-th number and there are more than less dp[i-1][s-j] < n numbers, the next digit will be j+1 or higher and you are looking for n — dp[i-1][s-j] numbers.
@tfg, I finally managed to understand your solution (not really intuitive). I think it would have helped to mention the following:
1) The last (leftmost) digit is being set to the value of "j".
2) The last coloumn (index = 10) in the constructed table is not exactly similar in meaning as the others. It seems that it is a sum of the number of all 1 to i-digit numbers with sum of digits = 10.
For example, i = 3, j = 10, dp[i][j] = 63 (which is not the total number of 3-digit numbers with sum = 10).
Also, is there a simple approach to come up with this intuition ?
You seem to have missed the part that I said "dp[i][s] = number of numbers with i digits (leading 0-s counts) and sum of digits s", "leading 0-s counts"
A simple approach to come up with this intuition is solving digit dp problems.
However the answer exceeds 10^18 when k=10^18 which will cause overflow in case of your solution. However, we can try something like this. https://mirror.codeforces.com/contest/919/submission/65572372
digit dp is way more faster:
https://mirror.codeforces.com/contest/919/submission/242635982
jinlifu1999
http://mirror.codeforces.com/contest/919/submission/34773513
http://mirror.codeforces.com/contest/919/submission/34770710
Same Solution. Different Verdict . What type of Judge ?
Java programs inherently use more memory than C/C++ programs. Using
System.gc()might help (it recommends invoking the garbage collector, but just likeinlinefunctions in C, there is no guarantee that it will happen).Java Compiler Automatically collects garbage whenever not necessary. So no need for any external Garbage Collector. And If Java Programs uses more memory Why There are no different memory limits for different languages ?
That's the thing, the java garbage collector is invoked whenever it "thinks" there's some memory to free, but that may not be immediately apparent to it (how does it know for sure you won't be needing this bit of memory in the future?).
System.gc()doesn't invoke an "external Garbage Collector", it invokes the normal java garbage collector (or at least it recommends its invocation), but it invokes it NOW (at the point of the instruction), not when the system finds it necessary.I've had some problems in the past where a well-placed
System.gc()made the difference between MLE and Accepted (I've also had situations where using that instruction made things worse... the gc is just very unpredictable).As for your second question, on some online judges there ARE actually different memory limits for Java :). There might also be some problems on codeforces which have different memory limits (not sure). Just not this one :)
By the way, in the Java solution you use
LinkedListto store the graph, whereas in the C++ solution you usevector, which is the equivalent ofArrayListin java. Not the same thing :). Linked lists inherently occupy more memory (there's pointers to be stored in addition to the data).I've replaced
LinkedListwithArrayListin your solution and it got accepted. As a general rule of thumb, never use linked lists unless you specifically need them for something (for example, deletion of elements form the middle).Just use C++, I used java in the past and it sucked.
The k=1 case in problem C does hurt lol. Got hacked, though my code is fairly straightforward still.
Also, is it a right way to solve D by merging strongly-connected components into one node and do the calculations? Just discussed with my friend and I haven't tried this approach.
In D, if you have a SCC of size > 1 then you have a cycle and just output -1. In the other case, every SCC must have size = 1 so there is no need to "merge" them, because is the same as using the original nodes.
So for your answer, I think it is valid but it is unnecesary :p
For a DAG, the number of strongly connected components is equal to
n (the number of nodes)To be precise complexity of brute force in B is O(ans * log(ans)) :D
Yeah, since you need to add all the digits, which requires logarithmic number of additions.
Разве при n>=p уравнения может быть верной ? ведь уравнения n*a^n mod p = b при n>=p можно представить так => (p+(n-p))*a^n mod p = b отсюда (p*a^n + (n-p)*a^n ) mod p = b а это можно представить так => ( p*a^n mod p + (n-p)*a^n mod p ) mod p =b => (0 + (n-p)*a^n mod p) mod p =b
= > ( (n-p)*a^n mod p ) mod p =b => (n-p)*a^n mod p =b , а если (n-p)>=p то можно сделать точно самое еще раз
а все понял , извините )
CANNOT UNDERSTAND WHAT IS WRONG WITH THIS CODE..ITS GIVING 0.00000 for the first test case...works fine on my compiler
include<stdio.h>
int main() { double n,m,a,b; int i; double min=100000; scanf("%lf%lf",&n,&m); for(i=0;i<n;i++) { scanf("%lf%lf",&a,&b); double c=m*(a/b); if(c<min) { min=c; } } printf("%lf\n",min); return 0; }What compiler are you using for submitting? You can also try to use cout, input/output is the only I see that could be giving the error
The code you posted works just fine. I submitted it now and got acc.
To print double you should use %f format specifier in printf due to floating point promotion in functions with variable number of arguments (printf is such a function). So I just deleted 'l' in "%lf" in printf and got AC: 34779977
%lfis the correct format specifier fordouble%fis the format specifier forfloatFloating point promotion means float gets promoted to double, which means you should always use
%lfinstead of%f(not the other way around). However, for that very reason, (for printf at least)%fis exactly the same as%lf. It's not that%lfdoesn't work due to promotion, it's that%fALSO works due to promotion.The above code works just fine (I submitted it and got ac, with
%lf, just like it was posted). No need to modify anything.EDIT: I'm talking about C++ 11 and later (I don't know the standard all that well for previous iterations). As I'm typing this it occurs to me the question was not meant for C++, but for C and it seems like %lf for printf does indeed cause undefined behavior for C90 standard and lower (but codeforces uses newer standard, so the posted code still gets accepted even with C compiler).
What I've written is just a simple way to remember where to use %f and where to use %lf. But the best way to remember that is to learn it.
I was talking about C11 standard of language C. I chose this standard because first submission of vivekchandela2 for this task used exactly this standard. Here you can check it: 34744000.
Try submit using a different compiler. Like GNU C ++ 11.
Please add Tutorial for Problem F as well.
FOR PROBLEM B hehe i stuck in the optimisation for this code ignoring that brute force can be run easily for this code ..i was just trying that for a no < 100 starting from ...
19 add 9 for every no to be build which is a perfect positive integer and for 91
ADD 18 to get 109 then again add 9 .... to get the last 190 then add again 18 to obtain 208 then add 9..... finally till now the factor which we are adding to obtain next term is 18 ..now when 208 is added with 9 so and so on till 280 is reached then increment factor with 9 and add 280+(18+9) since prev value of factor is 18 update it to 18+9
to obtain 307 goes till this series
until the last series becomes like this 901 910 then here factor will be 81
but for next term add (81 not with 9 but with 18) to get 910+(81+18) = 1009
then make factor -> 0 and again keep adding 9 to the nos till 1090 is reached then do the above firstly mentioned steps .. that is 1090+(factor+18) to get 1108 then add successivley 9 til 1180 is not reached and then factor will always be updated by 9 that is 1180+(value of factor till here +9) to get new value of next term having sum = 10
perform this till the new 2 term series is not obtained .. I have observe many things about numbers regarding this question but i am so sure some of the cases might not fit in my factor adding approach because in some cases i observed like 1801 1810 (when series like this ) i cant add 1810+(val of factor till here + 18) since it will not yield me the perfect positive integer some other cases also are hot handled by my optimisation but i want that someone plzz understand this and can do further optimise it without using brutforce till 1000000000000(as an estimate no)
Because this code will runs in O(k) iterations rather than some large estimate . Plzz ignore me if i said something wrong . plzz give feedback thnkss
can anyone please tell why am I getting TLE(in 15th test case) IN 4TH question ?
https://ideone.com/Kpl1jy
can anyone explain why I am getting tle on test case 32 in problem d(Java)? http://mirror.codeforces.com/contest/919/submission/34773289
update: same c++ solution of mine is got accepted but it is giving tle in java. link to c++ code http://mirror.codeforces.com/contest/919/submission/34778298
There should be a nice and fairly easy solution for problem E with generators (prime roots). We know which power of g is a, which one is g, so we are just left with a simple congruence on exponents. Finding stuff can be done in O (p) instead of writing some sqrt algorithms, because p is nice
kpw29 would you please explain in more details. i am very weak in maths.
Is the brute-force for B really O(answer)? I mean.. computing the sum of digita on n takes log(n) time does it not?
with base 10; that is at max 7, which can be considered a constant.
Time complexity is about infinitely large inputs, so you can't just say "it's considered" to be a constant. Though in this problem, it's indeed quite trivial, but it's still an O (answer * log (answer)) solution.
If the input is infinitely large, I don't think we should worry about complexity at all. It will just take infinite time not matter what the complexity is.
My point was that since the base is 10; its even smaller factor than our regular log2n
That's right. The factor is really small. However, mouse_wireless was talking about the complexity, not how much actual time it takes within the input range, and that is what it means.
Time complexity is about how the time "asymptotically increases" as the input increases infinitely. Therefore, it's about the algorithm itself, not about the actual time consumed for "some" inputs.
Bubble sort has worst case complexity of O(N^2). You can say that if N is like 3, the factor is very small so you can almost ignore it. But no matter what that N is, it doesn't change that the complexity of bubble sort is still O(N^2), because it's the property of the algorithm itself.
I see your point but you should choose correct words.
I was trying to tell mouse_pointer not to nitpick such a small factor but I guess lots of people are too sentimental about it.
My solution is O(answer) using O(answer) memory for memoization of the sum of digits. http://mirror.codeforces.com/contest/919/submission/34749833 :P
Can somebody elaborate on Div2E
I seem to be deriving j - i ≡ b·a - j(mod p)
Thanks!
Edit: They edited the editorial, all clear now :)
You are correct too, next line in the editorial explains your result.
You equation becomes:
j = b.a^-j + i*p (mod p)Edit: no this is wrong, should be
j = b.a^-j + (p+i) (mod p)(editorial is clearer now)Now read the next line in the editorial:
mkagenius sorry but I don't see your point ?
No, that’s wrong you cannot add p, 2p, ...., tp from thin air. Their mod p is not 0. They have to come somewhere from the equation.
It's like saying 2 = 2, 2 = 2 + 0, 2 = 2 + 2 * 0 ..., 2 = 2 + t * 0
We can add any multiple of p to both sides because any multiple of p is zero modulo p
in editorial i=y mod p and what is (i-y+p)%p stand for? why i-y?
They have updated the editorial, it should be clearer now.
finally ,it is really clear now
I didn't understand what they mean by looping section?
The given term n*a^n mode p has a period of p*(p-1) always (sometimes less, but definitely repeats after p*(p-1) terms)
Can someone tell me why my submission for C fails in TC 32 ?
Swap these lines:
and
My solution here for B is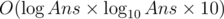
34769949
First, let’s binay search the answer x
Then our job is to check if there are more than k perfect numbers less than x
Let f(i,j) represent for the previous i digits, the sum is j, how many numbers can we have. Which is a classical digital dp.
I was retarded during the contest and thought k was smaller than 1e5, that’s why I solved B last and didn’t work out E, R.I.P.
You aren't the only one. Exactly same thing happened to me.
Why my code for D is giving wrong answer in TC 7. I used dfs to count the frequency in every path. In the worst case scenerio my code should give TLE, but I can not comprehend why it is giving me wrong answer. Here is my implementation.
Hi, maybe is because of the line vis[i] = true; in the for in solve function
Thanks. I see the mistake now. Anyway my way of solving this will give tle because of brute force approach.
yeah but it is not difficult to change, only add some memoization since the graph now is acyclic.
I am not that comfortable with DP, Can you show me how can I use memoization. [ I am aware of the concept]. Here is my TLE code. Thanks in advance.
this is my implementation.
So basically you try to count for every letter what is the maximum number of times can appear in any path starting at node u. And the maximum is the answer.
I hacked 2 people in problem C, because they're not careful when k=1.
I hacked 10 people in problem C, because they're not careful when k=1.
I was hacked immediately after I submitted problem C, for i'm not careful when k = 1.
Well...it could be worse, at least i have a chance to correct it.
I use dfs+dp in problem D. Dfs to find cycle. When there is a cycle, I will output -1. Dp to calculate which is the maximum number.
You needn't judge every number in problem B. You only need to judge x which x%9==1.
Can someone tell me why my solution for D fails?
What's wrong with this code?
460C
In your code, line 27...
Problem E was such a nice number-theory problem for beginners :D
In problem E, the 'looping' mentioned in the editorial mod p(p - 1) can be proved.
From Euler's Theorem,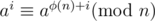 , for any integer n. Since φ(p) = p - 1, we only need to consider powers of a ranging from 0 to p - 2. This gives us two congruences:
, for any integer n. Since φ(p) = p - 1, we only need to consider powers of a ranging from 0 to p - 2. This gives us two congruences:
This system of congruences then has a unique solution mod p(p-1)), by the Chinese Remainder Theorem, which gives us the 'looping'.
Edit: Fixed formatting and notation: Fermat's Little Theorem -> Euler's Theorem.
Edit 2: The proof also gives a way to solve the problem using the Chinese Remainder Theorem, which is slightly different from the method mentioned in the editorial in its approach.
The idea follows directly from above: for each $i$ from 0 to p - 2 the above system of congruences can be solved uniquely mod p(p - 1), and the contribution of each of these to the final answer can be counted easily.
See 34764463.
In the editorial why did we take n = i*(p — 1) + j ?
Can anyone please help with Problem D... this solution is giving wrong on test 7.
The test case is huge to manually check it.
Thank you
http://mirror.codeforces.com/contest/919/submission/34794840
try this date case
5 5 abaaa 1 2 1 5 2 3 3 4 5 3
The true answer is 4
You did not think about the nodes you visited before(the nodes that visi[i] == true)
Try this:
: )
Auto comment: topic has been updated by jinlifu1999 (previous revision, new revision, compare).
could you tell the way on how to solve problem B by (dp+binary.s) or any other for BONUS 1 and 2
(sorry for my bad English :P)
Auto comment: topic has been updated by jinlifu1999 (previous revision, new revision, compare).
Can Someone please Explain E from expressing n as i*(p-1)+j.
Thank you.
Auto comment: topic has been updated by jinlifu1999 (previous revision, new revision, compare).
Can you please explain how did you get C(m+k-1,k) in F?
That is nothing but number of solutions to
x0 + x1 +x2+x3+ x4 =8 in this question. Similarly extend to general case
hey! can you please explain why i got a TLE error on this code? it seems pretty optimized to me! thanks :)
Passing vector dp by copy add & after vi.
What is looping section in problem E editorial??
The given term n*a^n mode p has a period of p*(p-1) always (sometimes less, but definitely repeats after p*(p-1) terms)
Actually, it will always be p(p - 1). Check my comment above for the details.
If the period was less than that, it would mess up the counting.
Edit: I was wrong, ignore this.
No, sometimes it repeats with period p*(p-1)/2 as well. Just check with 7 as P and 3 as A. And it won’t mess up your counting as it definitely repeats after p*(p-1) as well (coz divisible).
Huh. You're right, period p(p - 1) / 2 does occur sometimes too. My bad, then.
Your example is a bit wrong though. p = 7 and a = 3 still gives a period of p(p - 1). Instead, p = 11 and a = 3 gave me a period of p(p - 1) / 2.
Yeah, it was probably 7 and 2. Sorry I have a bad memory.
7 and 2 does indeed give a period of p(p - 1) / 2.
And yeah, counting doesn't get messed up because we're doing the counting mod p(p - 1) no matter what, so repeats within that will be counted separately.
For F,this is what you said: "First we should notice that the useful number of states isn't something like (8^5)^2" Maybe it isn't something like (5^8)^2,right?
can someone help me out ? I submitted problem D with my data structures statically sized using SIZE.I got MLE when my SIZE was 1000005 in the 6th test case. but when i changed it to 300005 I got AC. my question is , why didn't i get MLE in the first test case itself as the data structures are static? MLE :34803955 AC :34804264
So what's wrong? You were trying to allocate more than 256 MB memory (3 * 10^7 long long array is 230 MB).
why didn't I get MLE in first test case ? btw i allocated 1e6
Well, not all of your data structures are static. You have set ms; and you insert n elements in it, so in the first cases there is enough memory for your program. Why 1e6? You have ll dp[SIZE][30]; So you allocated 30 * SIZE = 3 * 1e7.
Can anybody give a proof why Problem D can't be solved using only DFS?. Keep counting the frequency of each letter in the traversal and record the maximum. -1 if cycle is found. I haven't solved it yet, but was wondering. Thanks
no , it can't be solved using DFS only. Take for example a graph with edges :1->2 , 2->3, 2->5, 3->4 , 4->6. As in DFS you only visit a vertex ONCE , the vertex 6 won't have the frequency table of 5 in it. the way i solved it was for every node , find the frequency table of its parent(s) and record the maximum. my code is kind of messy but the function you want to see is the dfs one. code : 34804264
In problem F, how to deal with cycles?
We don't need to do anything to that :)
Those which we don't meet in BFS (toposort) will be "DEAL".
BTW, You can give all states a "DEAL" tag for initialization.
can u go in more detail!plz
perhaps represent what u mean visually
In problem F,when current status is in circle,but I have other succeed status which are all lose states.Maybe I can go into one of the lose states and win instead of make it deal.With topological sort we can have the correct answer for this status,but what about the previous status?The previous status maybe not visited.How to deal with this problem?
Maybe only BFS is ok?
For Problem B. My Solution. Instead of iterating each and every value of n, I am finding the next Perfect Number in each iteration.
It came as a surprise to me when I found out
k=1was NOT in the pretests for problem C. I thought about trying to look for solutions which didn't treat this case but I thought surely it must have been in the pretests (usually pretests contain small cases like n = 0, 1, 2) so I decided to pass (I usually never go for hacks anyway, I prefer trying to solve more problems).Why the graph we built in F don't have any circle?
The graph may have cycles,but with topological sort we won't visit those cycles.
The states which were not visited will not be marked,so "Deal" only happens when ans[s1][s2]=0. But I think topological sort has a small problem,as I said here.
For problem F bonus, the answer is the number of non-negative integer solution of x0 + x1 + x2 + x3 + ... + xm - 1 = k.
It seems to be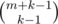 , and the number of status in the problem F is
, and the number of status in the problem F is 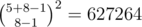 instead of 245025, right?
instead of 245025, right?
It is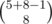 ,because the number of solutions of x0 + x1 + ... + xn = k is
,because the number of solutions of x0 + x1 + ... + xn = k is 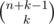 .
.
You can see it as combination with repetition.
Wikipedia has an article about this,see here.
Oh, I mixed up m and k. It should be . Thx
. Thx
Auto comment: topic has been updated by jinlifu1999 (previous revision, new revision, compare).
In the 2nd question, the code I've written works perfectly on my system, but when I uploaded it, it showed me a wrong answer. After the contest, when I executed the test case which went wrong on my own system, it showed the correct answer. Could anyone please help me in identifying the mistake?
1st submission: http://mirror.codeforces.com/contest/919/submission/35751191
^ Passed only the first test case
2nd submission: http://mirror.codeforces.com/contest/919/submission/35751331
^ passed two test cases, even though I changed just the starting number, from 19 to 1
both the codes are working perfectly on my system
sum() function does not return anything when s is less than 10, so the behavior is undefined in that case.
D is noice
For question F I am not quite sure why we had to run BFS (topological sort) on the graph? It is certainly cyclic. I tried DFS and got stack overflow but I am still not very sure where we got the idea to run the BFS from.
I started E without the assumption that p is prime(didn't read the question well) and voila! with 100% certainity that the answer was gonna be wrong yet submitted to find an AC!.
In problem E, there is a new algorithm that is newly developed called: "Chinese Reminder Theorem"
if anyone is looking for a digit dp solution for problem B then you can refer to submission
for further bigger value of k, you can also use BigInteger along with StringBuilder.