Результаты: http://opencup.ru/index.cgi?data=macros/stage&head=index&menu=index&stg=4®ion=main&ncup=occ&class=occ
Задачи: http://opencup.ru/files/occ/gp4/problems1-e.pdf
Кто знает, как решать F? У нас за n*logn с деревом интервалов TLE.
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Результаты: http://opencup.ru/index.cgi?data=macros/stage&head=index&menu=index&stg=4®ion=main&ncup=occ&class=occ
Задачи: http://opencup.ru/files/occ/gp4/problems1-e.pdf
Кто знает, как решать F? У нас за n*logn с деревом интервалов TLE.
| Название |
|---|



Как решать А?
Зашло не очень оптимальное решение примерно с 40^6 операциями. Выгодно покупать предметы слева направо. Динамика, где состояние номер предмета — id, кол-во денег — k ,сколько в предыдущих из (id+1, id+2, ... ) предметов были куплены, храним максимальный профит. Переход заключается в покупке нескольких предметов типа id.
Странно, у нас был TLE на 40^5, в итоге сдали за 40^4. Динамика такая же, переход за O(1).
обычная дп от 3х параметров (позиция, сколько осталось деньги, сколько товаров купили) — в ней храним оптимум. теперь идем справа налево и пересчитываем — пробуем в данной позиции купить сколько нибудь товаров. чтобы быстро работало, надо: а) заметить, что за 1600 монет всегда можно скупить все что есть, б) для троек (позиция, сколько купили правее позиции, сколько покупаем в текущей позиции) сразу посчитать сколько мы заработаем.
там еще есть подлянка с пониманием условия. там как бы 2 количества товаров на каждую позицию — сколько их реально осталось и сколько автомат "думает", что осталось. когда автомат выдает i-ый товар, то он у себя отнимает из виртуальных товаров только из позиции i (хотя реальные товары уменьшаются в нескольких местах). то есть если в какой то позиции на самом деле товар кончился, а автомат считает, что нет, то купить отсутствующий товар можно.
у нас лично этот момент съел час контеста. не понимаю как некоторые команды сдали эту задачу с плюса.
Если товар не кончился, а на самом деле кончился, то моно просто купить его пораньше.
Никакой подлянки нет — если покупать товары слева направо, то этой проблемы нет.
оу... кажется осознал.
то есть у нас было логически неверное решение, а решение задачи альтернативного понимания условия (не факт что верное) чудом совпало с верным решением исходной задачи.
жесть.
нифига себе. понятно. жестокая подстава. спасибо.
Как в Div.2 решать M и U ?
U Для начала научимся решать задачу для отрезка [1, r]. Сгенерируем простые числа до k + 1. Найдем всевозможные числа, которые являются произведением этих простых(каждое простое входит со степенью 0 или 1). Их не много, т.к. нужны числа только до 2e9. Теперь найдем количество составных чисел по формуле включений-исключений. Формула очевидна, если нарисуете круги Эйлера.
=)))) Ок, тогда ответ для (для отрезка [1, r]) k = 1: r / 2; k = 2: r / 2 + r / 3 — r / (2 * 3), и т.д.?
Еще надо вычесть кол-во простых до k + 1, которые попали в этот отрезок.
спасибо)
В дорешивание залил примерно такое решение:
всего пар может быть (N=n*(n-1)/2), значит различий в 4 символа можно не считать. (c4=N-c1-c2-c3)
для каждой строки строим маски, заменяя символы на *, например для dead — *ead, d*ad, d**d, d***, и т.д. всего получается 14(4+6+4) масок. для этих масок, создаем массив счетчиков для вида маски и какую-то структуру счетчиков по самим маскам(например, хэш-таблица).
при добавлении в хэштаблицу новой маски, которая там уже была, текущий счетчик маски плюсуется к виду.
после считывания всех элементов, собираем счетчики видов в 3 группы(4+6+4). Нужно, еще учесть, что в 3 группе есть пересечения с 1 и 2 группами, а во второй пересечение с 1й группой. эти пересечения нужно вычесть, вначале из 2, потом из 3. Тут я рисовал табличку с масками и по ней искал пересечения.
http://pastebin.com/fTp4nRtT — вот такой код на Java получился
ок, спасибо)
Как решать R и Q (div2) ?
Объясните, пожалуйста, в задаче О(div 2) как там получили 0,19 ?
0.1 + 0.1 — 0.1 * 0.1
1.0 — (1.0 — 0.1) * (1.0 — 0.1)
P(A + B) = P(A) + P(B) — P(A * B) Формула очевидна, если нарисуете круги Эйлера.
Как сдавали Е? У нас решение за О(p*p*26) получало ТЛ. Или это упихать можно?
вы видимо хранили в вершине дерева разбора d[v][i] — количество способов получить остаток i. Вот при пересчете для степени можно за O(p) для вершины посчитать, для суммы d[v][i] = d[left[v]][j] * d[right[v]][z], где (j + z) % p == i, так вот это можно посчитать с помощью FFT. А для умножения можно просто остаток заменить на степень, в которой первообразная равна этому остатку, тогда решение будет как и для суммы
Расскажите, пожалуйста, как решать B и K?
Если вкратце, то в задаче B делаем так: 1) Разбили все по слоям с одинаковой интересностью. Понятно, что в ответ войдет ровно по 1ой клетке из каждого слоя. 2) Будем считать ответ последовательно для каждого слоя по возрастанию интересности. Динамика: d[i][j] — ответ на задачу, если закончили в клетке (i, j). Тогда её пересчет — это просто максимум по всем клеткам из предыдущего слоя (динамики + расстояние до (i, j)). Получили переход за линию — медленно. 3) Пусть посчитали iый слой, тогда сделаем следующую структуру данных в 4х экземплярах: будем поддерживать максимум из (d[i][j] + (n — i — 1) + (m — i — 1)) (для каждого угла формулка своя, но схожая, так что будем рассматривать только случай верхнего левого угла)на префиксном прямоугольнике с общим верхним углом в углу нашего поля(4 угла — 4 разных версии). Для этого подойдет, например, двумерный фенвик. 4) Теперь пересчет динамики будет таким: просто возьмем очередную точку из i+1 го слоя, она делит на 4 префиксных прямоугольника наше поле, в каждом из них найдем максимум в соотв. фенвике, и из них выберем максимум. Получили сложность решения n*log^2 и ТЛ cоотв. 5) Теперь можно избавится от одного log, просто заменив одну координату пересчетом с помощью указателей. Посортируем клетки из iго и i+1-го слоя по x, при равенстве по y. Тогда идем сканлайном, фенвик будет по y-кам. Еще один вариант: заменить фенвика на дерево отрезков сетов и применить каскадирование(для особо изощренных). Ответом будет максимум по всем клеткам d[i][j]. Насчет задачи K: Утверждается, что выгодно всегда убивать только по отрезкам, в которых выстрелы расположены через 1(точка — тоже отрезок). Тогда происходит несложная динамика d[i][j][0..2] — i клеток обработали, j выстрелов сделали, 0 — выстрелили на предыдущей клетке, 1 — на предпредыдущей, 2 — не стреляли. Переходим за 0(1). Получаем квадрат состояний, переходы за 0(1). Насчет доказательства факта: нужно показать, что не будет встречаться двух подряд идущих элемента. Если нестрого, то если встречаем три подряд, то средний можно выкинуть, а вместо пары можно сделать пару со свободной клеткой(в которую не стреляли) между ними.
Ещё можно избавиться от второго log, если заметить, что достаточно просто хранить 4 максимума с предыдущего слоя.
Спасибо большое!
Про задачу F: В дорешивание сдалось решение за линию по времени и за O(1) по памяти.
Идём по позициям в порядке возрастания. Пусть в i-ой позиции записано число xi.
Если xi > si, где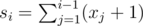 , то i-ю машину должны обогнать как минимум xi - si раз. Запомнили это количество (mi = xi - si) и позицию (pos = i).
, то i-ю машину должны обогнать как минимум xi - si раз. Запомнили это количество (mi = xi - si) и позицию (pos = i).
Иначе, если mi > 0 и xi ≥ i - pos (есть машина, которую надо обогнать и i-ая машина может это сделать), то уменьшаем mi на min(mi, xi - (i - pos) + 1) (догоняем i-ой машиной pos-ую и обгоняем её). Так как i-ая машина окажется впереди pos-ой, pos нужно ещё увеличить на 1.
Если после обработки n-ой машины mi > 0 (необходимы машины после последней), выводим , иначе —
, иначе — 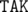 .
.
Отлично! Не очень понятно почему это работает, но вроде интуитивно это ощущается :-)
А как решать за nlogn с деревом отрезков?
Я правильно понимаю, что xi - si это сколько минимум раз нам нужно обогнать не "вообще", а машинами с большими номерами?
Когда мы вычитаем min(mi, xi - (i - pos) + 1), то этим мы как бы учитываем сразу несколько свопов машинки с номером pos и с номером i?
Да, именно с большими.
Основная идея этого вычитания минимума — мы обгоняем i-ой машиной pos-ую один раз и переходим к той же задаче, но перед машиной с позиции pos оказывается ещё и бывшая i-ая с некоторым запасом обгонов, которого не было раньше в spos.
Как решать задачи G, E?
В E парсим выражение, считаем динамику по дереву разбора: dp[v][i] — сколько способов получить значение i в поддереве с корнем v. А пересчитывать динамику с помощью умножения полиномов быстрее чем за квадрат.
UPD: для суммы понятно как полиномы построить, а для умножения логарифмируем и получаем сумму. еще в умножении правильно учесть случай с нулем.
G — добавление точки либо не меняет выпуклую оболочку, либо выпиливает и нее отрезок, и добавляет на его место точку. В первом случае площадь не поменялась, во втором — надо взять сумму векторных произведений на отрезке и что-то прибавить. Самое мерзкое — найти отрезок = касательные к многоугольнику. Про это выше уже кто-то писал.
Кто-нибудь знает, когда будет доступно дорешивание?
UPD. Уже доступно.
А за что заминусовали то? Дорешивание сейчас не работает.
Может, за некропостинг?.. Но мне показалось, что создавать новую тему из-за такого вопроса как-то глупо...