XVIII Open Cup Grand Prix of Korea takes place on Sunday, February 4, 2018, at 11:00 AM Petrozavodsk time.
The link to the contest.
The problems were prepared by kriii, ltdtl, .o. and me.
I hope you all enjoy the problems.
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
XVIII Open Cup Grand Prix of Korea takes place on Sunday, February 4, 2018, at 11:00 AM Petrozavodsk time.
The link to the contest.
The problems were prepared by kriii, ltdtl, .o. and me.
I hope you all enjoy the problems.
| Название |
|---|



Auto comment: topic has been updated by ainta (previous revision, new revision, compare).
Is it a closed contest? How to register for it ? My Yandex username password does not seem to work it says "Authorization failed. Please, try again or contact your coordinator"
What is Grand Prix?
I couldn't make much from that discussion...perhaps you can answer my question...
It is an onsite contest with multiple sites, called "sectors". You can't get a username/password to participate online, but you could try to organize a sector in your university/community.
Who are the relevant people to contact if I'd like to do this at my university?
The relevant page is http://opencup.ru/index.cgi?data=oci/rules/sector&menu=index&head=index&class=oci&ncup=oci . It's in Russian, but I hope Google Translate can help, and the email address (new.opencup...) is somewhat clear there.
On Codeforces the coordinator's handle is snarknews, but probably an email is a more reliable way.
Thanks,Petr
How to solve L and J?
Div.2 contest ended 40 mins later, hopefully no-one answered during contest time.
Problem + solution is more or less equivalent to problem E here: https://agc002.contest.atcoder.jp/tasks/agc002_e.
Surprised that not more teams solved it.
Do you mean it's equivalent to problem J of this contest?
Yes. Both of them can be transformed to a game about taking steps up and right in the coordinate plane, and in this problem (like the other one) one can prove that the answer for [L,R] is the same as the answer for [L+1,R-1] as long as the game is at least two turns away from the end.
I'm the author of problem J. I already knew the AGC problem, but I never noticed the equivalence relation. I think it is hard to find the relation between two problems without the key idea([L,R] = [L+1, R-1]).
Maybe that's true. For me, once I drew a diagram of state in the 2-dimensional plane, the connection came instantly.
Key idea what? Isn't it just ai = N - (maximum j s.t [i, j] is monotone for 1 ≤ i ≤ N?
Well, we have queries, but whatever...
Sorry about replying after 2 month. But when I try to upsolve this problem, I cannot figure out why Win[b, e] = Win[b + 1, e - 1] for other cases. Could anyone please teach me? Thank you.
Solution for J:
Let A[b, e] = ab, ab + 1, ..., ae.
For the initial sequence A[b, e], Win[b, e] = 1 if Alice wins the game. otherwise Win[b, e] = 0.
If A[b, e] is monotone(nonincreasing or nondecreasing), then Win[b, e] = 0. For other cases, Win[b, e] = (!Win[b, e - 1])|(!Win[b + 1, e])
Key idea : Except a few cases, Win[b, e] = Win[b + 1, e - 1]. then we can calculate Win[b, e] easily by its b + e value.
For a sequence S, if there is a contiguous monotone subsequence with length L and there is no contiguous monotone subsequence with length L + 1, we call S is L - monotone.
If A[b, e] is (e - b + 1) - monotone, then Win[b, e] = 0.
If A[b, e] is (e - b) - monotone, then Win[b, e] = 1.
3-a. A[b, e - 2] is monotone or A[b + 2, e] is monontone
without loss of generality, A[b, e - 2] is monotone. Then Win[b, e] = !Win[b + 1, e] = Win[b + 2, e] = !Win[b + 3, e] = .... it continues until Win[i, e] which A[i, e] is monotone. So if we precalculate L(e) := (the minimum value of x that satisfies A[L(e), e] is monotone) for all e, then we can calculate Win[b, e] by the value L(e).
3-b. A[b + 1, e - 1] is monotone
It is easy to show that Win[b, e] = 0
For other cases, it is easy to show that Win[b, e] = Win[b + 1, e - 1].
I think it's not true that we can calculate Win[b, e] in 3-a only from L(e), it depends on L(e - 1) as well. For example, consider this case:
1 2 3 4 5 5 5 5 5 5 4 5
Yes, I missed it. We can calculate Win[b, e] by the value of L(e - 1) and L(e).
Could you explain more about win[b, e] = win[b + 1, e − 1]? I could not understand how the formula in the pdf solution win[b, e] = (!win[b, e − 1]) | (!win[b + 1, e]) = (win[b, e − 2] & win[b + 1, e − 1])|(win[b + 1, e − 1] & win[b + 2, e]) would lead to win[b, e] = win[b + 1, e − 1]. What if win[b, e − 2] = win[b + 2, e] = 0, win[b + 1, e − 1] = 1?
Hint for N (div.2)? Output of test #1 given in example is incorrect answer for judge.
How did you solved it?
How to solve B, I?
Was problem I solvable with suffix array or suffix automata was intended? And how to solve F?
F: dp[mask][root] in O(3n * n2)
Is there any better solution for F?
Our solution in O(3n × n2) got TL on the first try. And, finally got an OK with some constant optimization.
intended solution is O(3n * n).
Could you please describe it?
dp[mask, root] = min{dp[mask^submask][root] + dp[submask][child] + cost(root, child) × popcount(submask) × (N - popcount(submask))}.
This is O(3n·n2), as you know -- 3n for iterating mask and submask, and n2 for iterating root and child.
However, min{dp[submask][child] + cost(root, child) × popcount(submask) × (N - popcount(submask))} only depends on submask and child. So precalculate them during the process, and it will reduce the complexity by n.
My recurrent formula in O(3n * n):
Nice!
I: Build suffix automaton for the whole string. After that you can start feeding string s to the automaton. If you go to the vertex v, this will mean that we added + 1 occurrence for all its suffixes.
Hopefully all such suffixes lie on path via suffix links of vertex v, thus you have to add + 1 on the path from v to the root (noting that any vertex u has multiplicity len[u] - len[link[u]]) and output sum of squares of numbers in all vertices taking into account their multiplicities. It can be done with heavy-light decomposition. Code: code.re/bbW
Can you somehow get rid of the HLD part ? maybe by flating the tree ?
I don't know. HLD part is very simple here, though, why would you want to get rid of it?
I is solvable with suffix array + divide and conquer.
The answer for a single string can be calculated if you know Sum(LCP[i, j]) for all unordered pair i < j. kriii will explain details / proofs in this part. We should solve this problem for every suffix.
One naive strategy is to build a suffix array sfx[], and LCP array lcp[] for a given string, then performing a[min(sfx[i], sfx[j])] += Min(lcp[i+1], lcp[i+2], ..., lcp[j]) for all i < j.
We can solve this by divide and conquer — We will process this for all pairs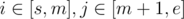 . The strategy is to batch process all pairs with same LCP value in "conquer" stage.
. The strategy is to batch process all pairs with same LCP value in "conquer" stage.
We start from m / m+1. If LCP[m] < LCP[m+2], then we increase right end, otherwise we decrease left end. To generalize. If current left end is s, and right end is e, then you know either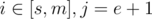 or
or 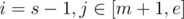 have same LCP value. (I strongly recommend you to simulate by hand). In the end, we end up having O(nlgn) "slices" to process.
have same LCP value. (I strongly recommend you to simulate by hand). In the end, we end up having O(nlgn) "slices" to process.
Now, we can process those slices with sweep line, in total O(nlg2n) time.
Nice explanation, thank you. Did not come to the last step with sweep line though.
Can you elaborate on how can you calculate the answer for a single string with Sum(LCP[i, j]) for all unordered pair i < j ?
What is test 53 for A?
That is the ordinary random case N=99998, L=94633361, R=475442794.
How to solve A and F?
A: For each point, the possible center of the donut to contain that point is also a donut. After adding each score to the corresponding region, the answer is the one with maximum score. It's equivalent to add the score to a square with length r and subtract the score to a square with length l.
It can be done with sweep line and segment tree in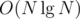 .
.
Very nice problems, thank you for preparing them.
You may check out short descriptions of the solutions for some problems.
I'm the author of problem ABFGIKL. Thank you for the participating contest.
I surprised that many Petrozavodsk camp teams solve K. I thought K will the most difficult in this set. Was there existed some similar problem in the past? Or was K straightforward?
How to squeeze FFT approach in L? I know that some participants done it..
Maybe you can try this one? (Didn't tested it though)
But well, I think squeezing FFT is not a good way to waste contest time / penalties.
K
But this problem allowed O(n * A3) solutions, which is definitely not the case for the tonight's problem
I wouldn't say that 3 teams is many.
What is the 2nd case of problem E?
I was wondering if there is any case to break following greedy solution:
When inserting x, find the furthest point y, that can be done by BS/set. Insert (x, y) into a PriorityQuery.
When deleting x, just delete it.
Now, when we query for the furthest pair, we look at the PriorityQueue head. 3 cases: 1. If (x, y) and both of them are alive then, this is the answer
If both of them are dead, just delete it and look at next pair
If one of them is dead, say y, then find the furthest pair with x. Delete (x, y) and insert this new pair. And continue looking at the head of PQ.
This solution gets WA in case 2. Not sure if there is anticase or I have bug in my code.
NVM. It works. I used find instead of lower_bound/upper_bound to BS in the set. Stupid mistake.
More detailed explanation of B?
I'm not sure if it helps, but it has some similarity with this this task, although this one is a lot harder.
I really liked the problemset, many thanks to the authors!
Why not apsolvingi?