hars123's blog

needed help in modular arithmatic.
By hars123, history, 7 years ago, In English

I am recently solving a problem to find a^(n!)%m and got stuck. please suggest how to solve this problem and some resources and problems to learn concepts related to modular arithmatic.

  • Vote: I like it
  • 0
  • Vote: I do not like it

Comments Comments (1)
| Write comment?
»
7 years ago, # |
← Rev. 2   Vote: I like it +3 Vote: I do not like it

What are the constraints for a, n, and m?

If a and n are small, and gcd(a, m) = 1 (a & m are coprime)

Then first, remember that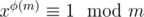 where φ(m) is the euler totient function of m. That means, we can simplify 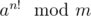to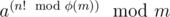

You can calculate φ(m) in O(sqrt(m)) and then calculate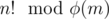 in O(n) and then the power with binary exponentiation in O(log2(m)) so the total complexity is O(sqrt(m) + n + log2(m))

→ Reply