I dont see any blog created for this contest.Also editorials seems to not be published yet.
My idea for E was bit long to code.But I see many people did it in short time.So can someone brief up with a good approach.
Also feel free to discuss other questions below.
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
31:14:52
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
31:14:52
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 10:20:10 (g1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Any hints for F??
I could make following observations
1. Analyse for 1st player in 1st position .And multiply answer by 2^n.
2. Instead of counting for correct permutations , may be try to do some bitmask dp to count wrong permutations(m<16 makes me think in this direction),I couldnt figure out how to do this??
I found rng58's analysis, even muted, pretty easy to understand: https://youtu.be/WFg2yJGZ2Cw?t=47m41s
My solution:
we can find N subtournaments of 20 to 2N - 1 players; player 1 plays against the winner — the smallest player — from each group, we need to ensure neither of them is one of the given M
there are too many choices of these smallest opponents, but we can use inclusion-exclusion — we only need to compute the number of tournaments in which the winners of |S| subtournaments belong to a subset S (of the given M opponents) for each |S|
if we fixed S, fixed the sizes of subtournaments won by members of S and went in decreasing order of numbers in S, this number can be computed as a combinatorial formula: for a given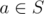 , if the subtournaments for previous (larger) numbers in S have total size x and its subtournament has size 2k, we're choosing 2k - 1 numbers out of 2N - a - x (all larger unused numbers) and then we have (2k)! ways to order them within the subtournament; at the end, there are 2N - 1 - x unused remaining numbers and we can choose their order in (2N - 1 - x)! ways
, if the subtournaments for previous (larger) numbers in S have total size x and its subtournament has size 2k, we're choosing 2k - 1 numbers out of 2N - a - x (all larger unused numbers) and then we have (2k)! ways to order them within the subtournament; at the end, there are 2N - 1 - x unused remaining numbers and we can choose their order in (2N - 1 - x)! ways
note that we didn't use the actual values larger than a in S at all, only the sum of sizes of their subtournaments, so we can turn it into a DP that counts the number of ways to use j numbers out of Ai..M as smallest numbers in subtournaments with total size x
since the subtournaments' sizes are powers of 2, x is also the bitmask of already used subtournaments, so we can transition from a state (i + 1, j, x) to (i, j + 1, x + 2k) if the k-th bit in x is unset
this gives O(M22N) states and O(M2N2N) transitions, each of which can be handled in O(1) if we precompute factorials and their inverses
How to solve D ? I got Ac till 21st case during the contest and WA on remianig cases. i took 100 X 100 2-D array , after that i divided my 2-d array in two equal halves.one half consisting of '#' and other of '.', so arr[1...50][1...100] consist of '#' and remaining of '.' after this I placed a-1 '.' in pool of '#'(halves of '#') with the condition that all the adjacent entries must be that of '#' and similiarly for '#' but i got WA ,after contest i tried to check on all the possible divison of matrix in to two parts (one of '#' and other '.') and place the a-1 '.' and b-1 '#' correctly but still got WA.
any hint or explanation for D. Thanks in advance
Presumably a similar idea: https://pastebin.com/XYvXUtXR
Please can you explain your train of thought in getting here , I was unable to come up with this solution in contest time , nice idea by the way!
If given A=1 and any number of Bs it is easy just to fill everything with A elements and make B number of holes (which do not disconnect A). The same goes for B=1 and any number of As. So by dividing the grid into two parts we can deal with A=1 and B=1. The extras could be turned into the holes mentioned. Actually, for similar problems I always think about chess board coloring at first, which was not suitable here. However, this led me to a much simpler division of the board :)
Thank you for your thoughts , I will keep this in mind , also , can you suggest me some good places to practice problems of the same type , greedy / constructive I feel I am very weak at these!
I can't help you with this, sorry :) The only area which I know worse than constructive algorithms is geometry. I guess that you could find some of the problems here, on CF. However, they are usually pretty rare.
After having a look at editorial and your solution .......my idea was correct but what my mistake was is terrible -_- . i took the up,down,left,right as only the adjacent elements not the other one's ...only one change and got AC
\(-_-)/.i'm also interested in a solution for E! Can someone help? (problem here: https://arc093.contest.atcoder.jp/tasks/arc093_c)
I will try to explain my idea.
I calculated for every pair of edges the min spanning tree cost containing those two edges.This can be done by using n min spanning trees for each edge and constructing the tree and using max queries on paths of trees.
Let val[i][j] denote min spanning tree cost containing ith and jth edge.now if val[i][j] < x then they both should have same colour.so join then (I used dsu here). After doing this we will get some components in which each must be colored with a single color.so 2^components will give number of ways to get min spanning tree more than equal to x.now similarly do last step assuming x=x+1.and subtract both which is required answer.
My solution for E is
Construct min spanning tree
Let W be weight of it. (Assume that W != X)
Then for each edge(u, v, w) that is not in spanning tree calc p = w — max_weight_on_path(u, v)
If we sort p's and pi is first edge with different colour with our spanning tree the weight would be W + pi
The answer is (2**(count of p such p == X — W) — 1) * (2**(count of p such p > X — W))
why is that if val[i][j]<x then they both should have same colour?also how are the components forming can u give a short reason ?
otherwise that spanning tree is a valid and has cost less than x.so we dont want them to be opposite color.So if val[i][j] < x.then they must be in same component. So if val[i][j]<x then merge them
Sorry for delay, uploaded the editorial.
It would be good if someone related posts a blog post here before contest.Last week I thought it was on Saturday(I was busy on Sat) and I missed it. But one of my friends said it is Sunday.