the constraints for n and k are upto 10^6. I wanted to efficiently precompute all the binomial coefficient (n choose k) and store them somewhere for further use. Please help me!. Thanks in advance!.
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | jiangly | 3977 |
| 2 | tourist | 3815 |
| 3 | jqdai0815 | 3682 |
| 4 | ksun48 | 3614 |
| 5 | orzdevinwang | 3526 |
| 6 | ecnerwala | 3514 |
| 7 | Benq | 3483 |
| 8 | hos.lyric | 3381 |
| 9 | gamegame | 3374 |
| 10 | heuristica | 3358 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 170 |
| 2 | -is-this-fft- | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 160 |
| 5 | djm03178 | 157 |
| 6 | Dominater069 | 156 |
| 7 | adamant | 154 |
| 8 | luogu_official | 152 |
| 8 | awoo | 152 |
| 10 | TheScrasse | 147 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jan/07/2025 06:43:25 (k3).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











That will require O(n2) memory which will surely MLE for n = 106. But you can precompute factorials and inverse factorials and store them in an array. Then after doing this you can calculate any binomial coefficient in O(1) time.
I don't understand what do you mean by inverse factorial when the question didn't mention taking modulo (it must be given, otherwise large answers).
Assuming modulo: Assuming modulo is a prime, use extended euclid or fast expoentiation for inverses else use Chinese remainder theorum to break modulo. Or lucas theorum may be used to break number in case of prime modulo.
You can't actually store them. You don't seem to have any idea how large it can be.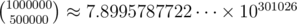
Example:
If you want to store all of them, then sum of number of digits will be approximately -
That is gonna cost you 300 GB of memory. Good luck finding that much RAM ;)
If you want them modulo some number then reffer to the above comment.