Question 01:
Is there any technique where generating random number within a range is equiprobable ?
Question 02:
What is the extra advantage of the following method 02,03,04 ?
srand(time(NULL);
//Method 01: general approach
int myrand(int mod){
return rand()%mod;
}
//Method 02: Taken form red coder submission.
int myrand(int mod) {
int t = rand() % mod;
t = (1LL*t*RAND_MAX + rand()) % mod;
return t;
}
//Method 03: Taken from red coder submission.
int myrand(int mod) {
return (int) ( (((double) rand() / RAND_MAX) * (mod) ));
}
//Method 04 : Taken from red coder submission.
inline int myrand(int mod) {
return (((long long )rand() << 15) + rand()) % mod;
}
Updated : Idea from diko.
auto seed = chrono::high_resolution_clock::now().time_since_epoch().count();
std::mt19937 mt(seed);
int myrand(int mod) {
return mt()%mod;
}










rand()returns a value between0andRAND_MAX. ButRAND_MAXcan be less than yourmod(eg on Codeforces it equals 32767), so Method 1 is wrong. There are two ways to fix it. First one is Method 2. Second one is usingmt19937instead ofrand(). (It returns a 32-bit random value). Method 3 is also wrong because it also returns only 32767 different values.I don't know how to generate it equiprobable, but these methods work almost equiprobable. I recomend using
mt19937because it works faster and more randomly.Method 3 is also wrong because it also returns only 32767 different valuesIt isn't wrong.
rand()/RAND_MAXis multiplied by the MOD under consideration, so it gets mapped to the range [0, MOD].A lot of numbers will never be generated with this function. For example, if mod = 106, this function can generate only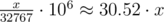 , where x is an integer between 0 and 32767. So, this function will never generate 1, 2, 3, 4, ... 29 and many others numbers. So this function isn't a random function in range [0, mod).
, where x is an integer between 0 and 32767. So, this function will never generate 1, 2, 3, 4, ... 29 and many others numbers. So this function isn't a random function in range [0, mod).
Also doing
gen()%modis not preferred you can usestd::uniform_int_distribution<>(0,mod-1) dis; dis(gen);