Hello Codeforces!
Lets discuss problems of the Poland contest. Any ideas on A? We came to the problem to count the number of minimal subsets with zero AND. How to count them?
| # | User | Rating |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
| Name |
|---|



Problem A: Let P0[i] = count of numbers i in array. Pk = Pk - 1 × P0, where × is multiplication of polynomials with AND applied to indices instead of sum (like it's described here, I don't know how to correctly name such multiplication). So the task is to find least k such that Pk[0] > 0, and answer will be Pk[0]·k!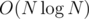 , where N = 220 , because k is limited by
, where N = 220 , because k is limited by 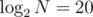 , and we can find Pk[0] in linear time, without inverse transformation.
, and we can find Pk[0] in linear time, without inverse transformation.
It can be done in
Any simple approach for B? We tried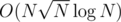 and got TL 52.
and got TL 52.
We had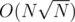 . We used Mo algo, but to maintain set size we didn't use set, just boolean array and current size
. We used Mo algo, but to maintain set size we didn't use set, just boolean array and current size
How to achieve with MO?
with MO?  is now feasible with original MO, but not
is now feasible with original MO, but not  .
.
That was a stupid typo,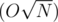 , ofc
, ofc
Sorry for being misleading
Thank you, I was just a bit confused :D
H ?