Привет, CodeForces.
Недавно решил поближе познакомиться с такой структурой данных как дерево Фенвика или binary indexed tree.
В данной статье я буду рассматривать дерево Фенвика для суммы, но все написанное легко обобщается на случай любой ассоциативной, коммутативной и обратимой операции.
Прочитав статьи о нем на e-maxx.ru и neerc.ifmo.ru и спросив друзей меня заинтересовал один момент. Обе статьи (и друзья) для инициализации этого дерева на заданном массиве предлагают создавать дерево Фенвика следующим образом:
- Деревом Фенвика для массива нулей будет массив нулей, возьмем его за основу,
- Далее запросами к дереву заменим все элементы исходного массива нулей на нужные нам и мы получим дерево Фенвика для нашего массива.
void init_vector_classic (vector<int> a) {
init_empty(a.size());
for (int i = 0; i < a.size(); i++) inc(i, a[i]);
}
Это работает за O(N * logN) от длинны исходного массива.
Можем ли мы делать это быстрее? Определенно можем!
По определению дерева Фенвика каждый его элемент представляет собой сумму на непрерывном отрезке исходного массива. Ввиду того, что запросы на изменение массива в процессе его инициализации отсутствуют, мы можем использовать частичные суммы для определения элементов дерева Фенвика. Это потребует препроцессинга O(N), но позволит определять элементы дерева за O(1). Таким образом асимптотика улучшится до O(N) + O(1) * O(N) = O(N).
void init_vector_linear_prefix (vector<int> a) {
init_empty(a.size());
vector<int> prefix_sum;
prefix_sum.assign(a.size(), 0);
prefix_sum[0] = a[0];
for (int i = 1; i < a.size(); i++) prefix_sum[i] = prefix_sum[i-1] + a[i];
for (int i = 0; i < a.size(); i++) {
int lower_i = (i & (i+1)) - 1;
fenwick[i] = prefix_sum[i] - (lower_i >= 0 ? prefix_sum[lower_i] : 0);
}
}
Но в такой реализации мы получаем дополнительные O(N) памяти на хранение массива.
Можем ли мы этого избежать? Можем!
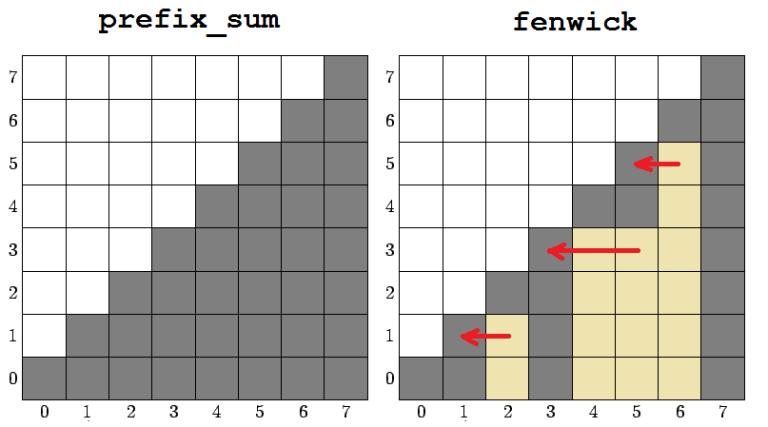
Заметим, что для инициализации fenwick[i] нам могут потребоваться только такие элементы prefix_sum[j], где j ≤ i. Это дает нам возможность использовать только один массив и, начиная с конца, постепенно переводить его из префиксных сумм в дерево Фенвика.
void init_vector_linear (vector<int> a) {
init_empty(a.size());
fenwick[0] = a[0];
for (int i = 1; i < a.size(); i++) fenwick[i] = fenwick[i-1] + a[i];
for (int i = a.size()-1; i > 0; i--) {
int lower_i = (i & (i+1)) - 1;
if (lower_i >= 0) fenwick[i] -= fenwick[lower_i];
}
}
Таким образом мы можем улучшить время инициализации дерева Фенвика до O(N) используя O(1) дополнительной памяти.
Конечно, в большинстве задач кол-во запросов к дереву Фенвика примерно соизмеримо с его размером, потому улучшение времени его инициализации не улучшит итоговую асимптотику решения. Однако такая оптимизация дает возможность уменьшить константу той части вашего решения, которая работает с деревом (или деревьями) Фенвика, путем добавления совсем небольшого объема кода.
Что вы думаете по этому поводу и как вы инициализируете свои деревья Фенвика?
UPD: Существует другой подход к этой задаче, который позволяет добиться еще меньшего объема кода! Спасибо, Jakube за комментарий об этом и sdnr1 за написание блога об этом.











I'm also using a linear time construction for the Fenwick tree (although I haven't used a Fenwick tree in ages). Learned the method from Is it possible to build a Fenwick tree in O(n)?. This method approaches the construction of the array from the exact opposite direction.
Auto comment: topic has been updated by ATSTNG (previous revision, new revision, compare).
I think it is still $$$O(n)$$$ additional memory on it since you copying a new vector to the parameter
I prefer to use this
I am not sure why I am getting downvotes. I dont mind having nagative contribution but atleast can some one explain me about my mistakes ?
Because as what I can observe the code below will create a new array. And the additional memory complexity will raise to $$$O(n)$$$ and not $$$O(1)$$$.
While using reference or const-reference wont create a copy to the parametter so it should be $$$O(1)$$$ additional memory
What would happen if I use other function then just summing up elements, is there any dangerous corner cases or something ? Because I dont think there are always existing inverse function like adding $$$(+)$$$ have its inverse: subtract $$$(-)$$$ so it is better to build things bottom-up right ?
Does this function correct ?