hmehta's blog

Topcoder SRM 734
By hmehta, 6 years ago, In English

Topcoder SRM 734 is scheduled to start at 21:00 UTC -4, May 16, 2018.

Featured Problem Writer: Vasyl[alphacom] [Profile](http://www.topcoder.com/members/Vasyl[alphacom])

You will be able to register for the SRM in the Arena or Applet 4 hours prior to the start of the match. Registration closes 5 minutes before the match begins, so make sure that you are all ready to go.

Don’t know how to compete in Topcoder SRMs?

Topcoder Java Applet — You can refer to this guide here to set up the applet. (Note that those who have Java 8 installed on their machine will see a security issue — You will have to add Topcoder in security exceptions in Java Control Panel. Please refer to the details in the guide)

Hope to see most of you competing! All the best!

  • Vote: I like it
  • +32
  • Vote: I do not like it

Comments Comments (11)
| Write comment?
»
6 years ago, # |
  Vote: I like it +3 Vote: I do not like it

The writer is Vasyl[alphacom]? That's good, I'm really waiting for interesting tasks!
By the way, the time in this blog and in the timeanddate link is different, isn't it?

→ Reply
»
6 years ago, # |
  Vote: I like it +8 Vote: I do not like it

Video solution to Div II P1 — TheRoundCityDiv2: https://youtu.be/RzobVOY4Qb8

→ Reply
»
6 years ago, # |
  Vote: I like it +13 Vote: I do not like it

How to solve Div 1 300?

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it +13 Vote: I do not like it

    WLOG we can just consider x, y > 0. A coordinate (x, y) is visible if and only x and y are relatively prime. So for each x coordinate, we want to compute the number of y s that are relatively prime to x in the range .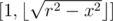

    We can use inclusion-exclusion to count everything that shares at least one factor with x and subtract these from the range. First we count all multiples of p where p is some prime factor of x. But this double-counts multiples of pq, so we subtract all multiples of pq. And then we add back multiples of pqs, and subtract multiples of pqst, and so on. So the total runtime is around

    Where ω(x) is the number of distinct prime factors of x. One piece of number-theoretic intuition is that ω(x) grows extremely slowly (maxx ≤ 1000000{ω(x)} = 7), and most elements in the range only have  ≤ 3 distinct prime factors. So this is fast enough in practice. (You can just run the maximal case to make sure.)

    → Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it -27 Vote: I do not like it

The Div2 contest was not good. It didn't have unique problems.

250 — google search "lattice points within a circle"

500 — brute force(low constraints)

1000 — standard dfs/dp travel in a grid with some conditions

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    I saw these Div2 problems, and I thought it's okay. Here's my feedback:
    250 — Div2 250 should be (usually) easier than CF Div2 A. Therefore, if they want to publish the simple problem, it's inevitable. And the importance in Div2 250 is to implement a program. No reason to complain.
    500 — I think its difficulty fits Div2 500. Although there is no "innovative" idea in this problem, it's Div2 and not hardest therefore it's okay. (One example of "innovative idea" in Div2 Medium is, SRM 726 Div2 Medium — TurtleGame, but the ratio of correct submission by participants were desperately low.)
    1000 — It's standard for red coders, but it's not standard for Div2 peoples. So you should go to Div1.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +6 Vote: I do not like it

      1) 250 is not easier than Div2A but okay, its hard to make very easy problems :P

      2) I didn't say problem was easy but just like you said it was not innovative.

      3) I thought travel inside grid is standard/common. These types of problems even have tutorials like third problem here and here. We just take some additional parameters in dfs to check for the conditions. That's all. About the Div1 thing, I hope this could happen.

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +8 Vote: I do not like it

        Yes, so your issue about Div2 250 and Div2 500 is solved :) Now we should talk about Div2 1000.
        Seeing rate of accepted people by number of participants, it is definitely "easy Div2 Hard" but not too easy. It's kind of a variation of "classic" problems, but I think it is normal in computer science world because most problems are continuance (or steps) of classic thinking. But hoping to see next SRM Div2 Hard to be interesting :)

        By the way, in similar (?) topic, I wrote a topcoder forum article about division cutoff and problem difficulty placement. I want all of your opinion. Please reply in this forum if you can :)

        → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone explain the Div1 Medium (CardCounter) solution please?

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    This is probably pretty late but here goes:

    The main observation is that the number of states <Your Hand, Dealer Hand, Deck> is pretty small since the deck only has 16 cards. (Note you can assume that the dealer starts with only that one card, and the unknown card is drawn next).

    With this observation you can just do a backtracking, while memoizing the already computed states. If you didn't stop hitting, you look what has a higher change of winning, either stopping and letting the dealer go, or continue hitting. If you did stop hitting the dealer's probability is a just simulating him in the backtracking.

    → Reply