UnfilledDreams's blog

Number Of Multiples.
By UnfilledDreams, history, 7 years ago, In English

I was solving a problem but I couldn't solve that problem.
Given an array of N elements, we have to answer Q queries in each query two number i and X will be given we have to find how many multiples of X will be there in the array after the ith (including i) index. The range of N, Q is 10^5 and same for the array elements.
Please help me out with the logic.
Thanks in advance.

  • Vote: I like it
  • +13
  • Vote: I do not like it

Comments Comments (11)
| Write comment?
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by UnfilledDreams (previous revision, new revision, compare).

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +14 Vote: I do not like it

I'll just determine T = 105 to ease on writing, then we can say that Ai, N, Q ≤ T. What I currently have works in total time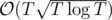 , if I'll find a better one I'll add it.

Since you're asking for "logic", I'll say how I think you should come up with this idea:

First, let's see that we can have multiple ways (though most of them are inefficient) to approach the queries, we'll focus on 2:

  • We can do some preprocessing: for each value and each index, we can precompute the answer for the query on that value and position. The total query time is and the preprocessing is .
  • We can do a different type of preprocessing: For each value in the array, we maintain a vector of its indicies in the array (also sorted; we just iterate from beginning to end). Then for a given X, i, for each multiple of X we do binary search on its vector of positions, to see how many indicies there are, which are at least i. This takes a total query time (in worst case) , and preprocessing .

The point is that approach 1 is heavy on preprocessing and light on query time, while approach 2 is the opposite. We can merge them. Let's determine a constant K:

  • We will do approach 1 only on values that are less than K, and for queries with X < K we can solve them by approach 1. The total query time is while preprocessing is .
  • We will do approach 2 only on values that are at least K, and solve with that queries for which X ≥ K. For some X in a query (which can be up to T) we binary search times, which is the worst case for X = K, so the total time on queries is and preprocessing is .

We want to pick a K for which the worst case between approach 1 and approach 2 is minimized. as K increases, approach 1 gets worse while approach 2 improves, so we would like to find a K for which approach 1 = approach 2:

: for this K, both approaches do in worst case total, .

Hopefully I didn't do too much :). This is pretty much sqrt-decomposition, but following only the idea and not the "sqrt" part.

Edit: one more thing to notice is that apporach 2 alone is worse than doing a simple brute force, but it's better in a sense because it can be easily improved using the constant K (which doesn't affect the brute force approach).

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +18 Vote: I do not like it

    Here's a simpler solution that works in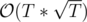 . I still think the above idea is good to know as it implies to a lot more problems.

    We'll make Ix be the vector of (sorted) indicies in the initial array, such that all the values in these indicies are multiples of x. We can preprocess all that in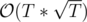 . Then for each query (x, i) we do binary search to find how many values in Ix are at least i. This is 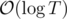per query.

    Though this is simpler and works in a better time complexity, I think the first approach I gave is good to know in general.

    → Reply
»
7 years ago, # |
  Vote: I like it +15 Vote: I do not like it

A simple solution here:

For each number precompute a vector of its divisors —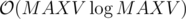 . Keep an array C[i] = number of multiples of i. Now we start from the end of the array and answer all queries such that their i is equal to the current index we are looking at. Answer will obviously be C[X]. Also before answering the queries add +1 to all divisors of a[i]. The complexity is .

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

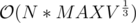    Thank you for helping me.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Scube96 Can you provide the link to the problem??

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        Sorry, I don't have the link of the problem this question appeared in an exam which was taken in proctored mode, so they didn't make that public.

        → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    How is total complexity calculated?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +10 Vote: I do not like it

      This should help you:

      Number X has approximately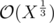 divisors.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
        ← Rev. 2   Vote: I like it +18 Vote: I do not like it

        On this topic, why do a lot of people use that statement? The exponent isn't really a constant one, it depends on X and decreases as X increases. Like, I can also state that the average number of divisors for a natural number up to X is 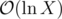(and, I think that as X becomes much larger, the worstcase number of divisors for a value up to X might also be ).

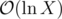        As an example, here are a couple highly composite numbers:

        • X = 2520, number of divisors is 48, around .
        • X =  9.77 * 1010 (largest highly composite up to 1011), number of divisors is 4032, around .
        • X =  7.8 * 1029 (largest highly composite up to 1030), number of divisors is 13271040, around .

        Edit: maybe this term is used a lot because the values we work here with are up to 1018...? So just for smaller values it's around square root and for larger it's around cube root.

        → Reply