A. Martadella Strikes Again
if R * R > 2 * r * r print 1, otherwise print 2
R and r should be long long or double to avoid overflow
B. Amer and Graphs
Since the edges are undirected ,we can store the edges {u, v} as (u ≤ v) for every edge (1 ≤ i ≤ n).
Let's assign a unique number for every unique edge in the array, then our problem will be reduced to :
Find the number of different segments of the array which have the exact same elements ( same frequencies as well for each element ).
This problem is a classic hashing problem that can be solved this way :
let's choose some random large prime numbers P and MOD ,for example P = 304933, MOD = 109 + 7.
replace every element {xi} from the array with Pxi%MOD.
now the final problem is about finding different segments of the array which have the same sum value %MOD .
This solution will get "Wrong Answer", so you need to do a double-hashing in the same way using other numbers P2, MOD2
Time Complexity : O(n2 * log(n)) .
C. Help Shahhoud
We greedily iterate from the sides and when two items need to be reversed we reverse the whole segment that contains them and add one to the final answer
If they can’t be equal even if we reverse them then it is impossible and answer = -1 .
We only need to keep a flag for the current state :
0 means the segment between the 2 pointers is not reversed.
1 means the segment between the 2 pointers is reversed.
D. Simplified 2048
The main idea is that we only need to keep track of the number of active cells and the last strictly increasing sequence of powers from right to left, this is because if we have a cell with number X and the cell to the right has number Y where Y > X , these two cells will never merge and therefore anything to the left of them won't add anything to the score so we don't need to keep track of them.
This leads to a DP Bitmask solution where we store the bitmask of available powers of 2 (they are guaranteed to be strictly increasing from right to left because we ignore any powers that aren't) and the number of active cells (free cells + number of bits in the mask).
If the current mask is msk and a 4 is generated, the new mask will become msk + 4 and ((msk)^(msk + 4)) - 4 will be added to the score.
When a 2 is generated, the new mask will become msk + 2 and ((msk)^(msk + 2)) - 2 will be added to the score.
The added score explained above is the score added from all the merge operations that will happen after adding the new number, not only the first one. Merging them all at once will not affect the final answer.
^ is the bitwise XOR operator.
E. Floods
The answer is the sum of areas of zero or more simple polygons that keep rainwater.
We will explain an easy way to find these polygons and then calculate their areas.
Look at the picture while reading for better understanding :
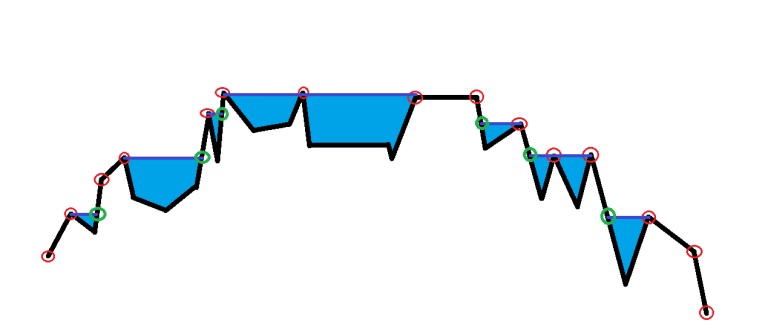
We will say that a point is important if it isn't underwater(red points in the picture ).
We can easily determine if the i - th point is important if it has the maximum value of y-coordinate from the first i points or the last N - i + 1 points of the polyline.
Any other point will have one or more points on it's left and one or more points on it's right with larger y-coordinate , so it will be underwater for sure (this point will not be important for us for now).
Now for every important point let us draw a horizontal line to the left (or to the right) to find the intersection point with some segment of the polyline (green points in the picture ).
We need to handle the 2 cases (when to draw a line to left and when to draw a line to the right).
The problem now is reduced to calculating the sum of areas of the resulting polygons.
Time Complexity : O(N)
F. Random Sort
let cnt[x] = number of occurences of x in the array
the answer is the multiplication of factorial$( cnt[x] )$
G. Weird Requirements
The problem asks you to make the minimum number of changes on the array to make GCD of all elements equals to X and LCM of all elements equals to Y.
First of all, let's count the number of elements that must be changed and call it C i.e. the elements where Ai isn't a multiple of X or a divisor of Y.
Note: the GCD of a group of numbers is the product of the common prime factors with the lowest power, and the LCM of a group of numbers is the product of all prime factors that appear in the numbers with the highest power.
There are 5 cases to handle :
1) Ans = - 1: if ( Y isn't a multiple of X ) or ( N = 1 and X ≠ Y ).
2) Ans = 0: if C = 0 and GCD(Ai) = X and LCM(Ai) = Y
for all (1 ≤ i ≤ N)
3 and 4) Ans = 1: if C = 0 and there is an element Ai satisfies the following condition or C = 1 and the element that must be changed satisfies the following condition:
Let's first factorize both X and Y.
The element satisfies the condition if after deleting it, each prime factor that appears in X or Y, must satisfy the GCD OR the LCM rule from the note above in at least one of the remaining elements. This way, if either the LCM or the GCD rule is not satisfied, it can be fixed by changing the deleted element. We can't fix both the LCM and GCD rule for some prime factor by changing one number, unless the power of the prime factor is equal in both X and Y (this case should also be taken care of).
5) Ans = max(2, C): otherwise
H. Shahhoud the Chief Judge
First of all, you need to calculate this dp :
dp[u] = the number of paths that includes node u.
The solution has three cases:
case 1: Ans = 0
calculate S = sum W[u] * dp[u]
if S = 0 then the Ans = 0.
case 2: Ans = 1
a node u is a solution if and only if ( S mod dp[u] = 0 )
let x be the new weight of u
0 = S — dp[u] * W[u] + dp[u] * x
=>
x = W[u] — S / dp[u]
which is an integer
case 3: Ans = 2
for each pair (u,v) if gcd(dp[u],dp[v]) = 1 then they can be an answer because:
( let's say that x, y are their new weights respectively )
0 = S — dp[u] * W[u] + dp[u] * x — dp[v] * W[v] + dp[v] * y
=>
a*x + b*y = c therefore such x and y always exist
and the pair (u,v) always exists because:
let u be a node with biggest possible depth, hence u is a leaf, and its other
sibling is also a leaf (it has a sibling because the tree is binary, and its sibling doesn't have any children because u is of maximal depth)
now if we look at dp[u] and dp[parentOf(u)] :
dp[u] = (n-1) * 2 + 1 = n-1 path ends at u with two directions + one path from u to u
dp[parent] = 6n - 11
and we have gcd(2n - 1, 6n - 11) = gcd(2n - 1, 6n - 11 — 3 * (2n - 1) ) = gcd(2n - 1, - 8) = 1
2n - 1 is odd, 8 can be only divided by 2.
I. Ildar Yalalov
The winning states are:
1) N is odd and sum(Ai) is odd.
2) N is even and at least one of sum(Ai) and min(Ai) is odd.
Let's look at the optimal strategy for Yalalov in the winning states:
1) N is odd. In this case, the number of stones removed in each step is always odd (either 1 or N). This means that the parity of the amount of stones left will flip in each move, so if sum(Ai) is odd, then there will always be an odd number of stones in Yalalov's turn, and since the losing state has an even number of stones, Yalalov will never reach the losing state so he wins. Otherwise, he will lose because he always ends up in a state with an even number of stones.
2) N is even and min(Ai) is odd. If sum(Ai) is odd, then the optimal strategy would be to use a move of the first type on the pile with the minimum number of stones, leaving an even number of second type moves, and an odd number of stones for the second player (losing position). The only way for the opponent to leave the losing position is to use a move of the second type, but you can negate the effect of it by using another move of the second type (there is an even number of them). When sum(Ai) is even, the best strategy is to use a second type move, leaving your opponent with an even number of stones, and and even number of second type moves, which is also a losing poition.
3) N is even and min(Ai) is even. If sum(Ai) is odd, the best strategy is to use first type moves, unless your opponent uses a second type move, you then also use a second type move to negate it's effect. If sum(Ai) is even, this is a losing state mentioned above.
J. Saeed and Folan
Since K is small, you can just simulate all the movements for both Saeed and Folan and add 1 to the answer when their positions are equal.
In each second, you need to first fix the direction of movement (if the person is currently at position L then the direction should be right, and if the person is currently at position R, the direction should be left), then move 1 step in the current direction.
After each step, check if the positions are equal.
Time Complexity : O(K)
K. Another Shortest Path Problem
The first thing to notice is that an undirected connected graph with N nodes and N edges has exactly one cycle and each node on this cycle can be a root of a tree.
Delete any edge from the cycle, let's say it connects nodes u and v with weight w.
The resulting graph is a tree. There are 3 cases for the shortest path between X and Y.
1) It does not pass through the deleted edge. So the shortest path is equal to the distance between X and Y in the resulting tree.
2) It passes through the deleted edge from u to v. So the shortest path is equal to the distance between X and u in the tree + the distance from v to Y in the tree + w.
3) It passes through the deleted edge from v to u. So the shortest path is equal to the distance between X and v in the tree + the distance from u to Y in the tree + w.
So, in each query, we take the minimum between the previous cases.
Note:
To find the shortest path between any two nodes in a tree:
First, consider any node to be the root, and calculate the distance from each node to the root in O(n) with a simple dfs.
Next, you can find the distance between any two nodes in a tree in O(log(n)) using LCA.
dist(a, b) = distToRoot[a] + distToRoot[b] - 2 * distToRoot[LCA(a, b)].
Another solution finds the cycle and finds the best way to go around the cycle using prefix sum for queries that are in different trees.
L. V--o_o--V
Coming Soon.











H, I are cool observations.
G test data is: 2 2 8 4 18 why the code output 1?
how to solve L ?