Здравствуйте!
Не так давно столкнулся с двумя задачками, связанными с перестановками. Решить их у меня не получилось, но мне бы хотелось разобраться, как решать задачи такого типа за полиномиальное время. Прошу помощи.
1) Условие: Дано число n и массив b — некая перестановка чисел от 1 до n. Нужно найти какую-нибудь перестановку a (также из n элементов), чтобы для каждого i (1 ≤ i ≤ n) выполнялось равенство b[a[a[i]]] = i. К примеру, если нам дана перестановка b = (3, 4, 1, 2), то в качестве ответа можно вывести перестановку a = (2, 3, 4, 1). Если искомой перестановки a не существует, вывести "0".
2) Условие: Из заданной перестановки нужно извлечь квадратный корень. Здесь можно прочесть полное условие этой задачи (задача P).
Заранее всем спасибо!
Наблюдение 1: Задачи решаются одинаково. Необходимо лишь заметить, что первой задаче требуется найти квадратный корень из перестановки, обратной к b.
Наблюдение 2: Для любой перестановки она разбивается на циклы различной длины. При этом после возведения в квадрат циклы нечётной длины сохраняют длину, но меняют порядок, а циклы чётной — разбиваются на два цикла равной длины.
Пример: (2, 3, 4, 5, 1)2 = (3, 4, 5, 1, 2) — тоже цикл длины 5. (2, 3, 4, 1)2 = (3, 4, 1, 2) — получилось два цикла длины 4/2=2.
Отсюда имеем: Каждый цикл чётной длины мог получиться только из большего цикла чётной длины. Значит, таких циклов должно быть чётное число. Группируем их по два (одинаковой длины) и составляем из каждой пары один больший. Каждый цикл нечётной длины мог получиться из такого же, поэтому просто переупорядочиваем его элементы соответственным образом.
Спасибо за ответ. Я не совсем понял, каким образом нужно переупорядочивать элементы нечетных циклов.
Ну вот смотрите.
Пусть у нас цикл 0->1->2->3->4->0. Он при возведении в квадрат становится циклом 0->2->4->1->3->0. Можно заметить, что элементы умножились на 2 по модулю длины цикла, то есть 5. Значит, чтобы найти корень, надо поделить элементы на 2 по тому же модулю.
Спасибо!
Здесь есть описание как найти корень с перестановки.
А как найти корень из перестановки произвольной степени? То есть если дана перестановка Y и число k, как найти такую перестановку X, что Xk = Y?
Похоже, что примерно так же.
Если у нас есть цикл длины n, то k-тая степень разбивает его на g=GCD(n,k) равных. То есть мы просто собираем g-шки циклов длины n/g и формируем из каждой один большой длины n.
Теперь вопрос о g-шках. Пусть для какой-то длины n у нас получилось q циклов. Тогда q надо представить в виде суммы qi таких, что k кратно qi и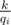
взаимно просто с n. Пусть g — минимальное такое число (его можно получить, взяв из k все простые делители n в максимальной степени) Все qi должны делиться на g. Значит, q должно делиться на g. Если это так, то берём g-шки таких циклов и склеиваем из каждой один большой, иначе — говорим о невозможности такого.
Например: Пусть k=6, а циклов длины 2 у нас вышло 8. Тогда мы можем брать по 2 таких цикла и по 6. Можно проверить, что циклы длины 2*2 и 2*6 в 6-й степени разлагаются на циклы длины 2, в то время как остальные циклы длиной 2*n этого не допускают.
А кто-нибудь может пояснить суть вот этого кода, решающего данную задачу?