Given an array of n positive integers called a
For each of q queries which are described with integers 1 ≤ l ≤ r ≤ n, output xor of unique values in segment(l, r), i.e. if x1, x2, x3, ..., xk is set of unique values from al, al + 1, al + 2, ..., ar - 2, ar - 1, ar, then output x1 xor x2 xor x3 xor ... xor xk
1 ≤ n, q ≤ 106
for all i, 1 ≤ ai ≤ 109
TL: 3.5 seconds
ML: 256 megabytes
How to solve it?
If it's possible, I'd like a solution which uses some of data structures listed below:
Segment Tree
Binary Rise/Lift
Trie
Merge Sort Tree
I think, it can be solved with MO`s algorithm and hashset.
Or without hashset using coordinates compression.
I think you can avoid hashes / set by applying coordinate compression on the array, while maintaining original values to be able to also compute the xor. This way, you can just keep an array of size N to keep frequency of each value.
This will have time complexity of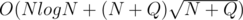
which I'm not completely sure may pass as N ≤ 106 usually requires O(NlogN) solution, but you should try it anyway as 3.5s is larger than usual time limits :)
you can use ofline segment tree for optimize solution.
Can You please further explain how can I apply it?
This is 703D - Mishka and Interesting sum. Sqrt-decomposition solutions generally don't pass in this problem, unless you use fast I/O and coordinate compression.
I assume what you mean is that given a range [l, r], the answer is as if we insert all these elements into a set, and then compute the xor of all values in the set.
Construct an array B from A: Bi = j, such that j is the last index in A in which we've seen the value Ai, or -1 otherwise. (Formally, such j that Aj = Ai, Ak ≠ Ai, for j < k < i, or -1 if no such j exists). You can construct this in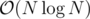
.
Now the task becomes "Given a range [l, r], compute the xor of all Ai for which Bi < l". This can be solved with a merge sort tree in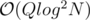
(make the tree of pairs (Bi, Ai), keep it sorted by Bi, and then each query requires binary searches on 
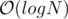nodes in the tree, while after each binary search you need to compute the prefix xor of Ai in a specific node, so you can preprocess prefix xors for all nodes in the tree).
You can also solve it in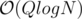
using a wavelet tree.
Doesn't such j always exist, since j ≥ i and Aj = Ai?
No, read more carefully. Noam defined it with j < i.
Does he mean last j < i, that Aj = Ai?
He meant last j before i. Look at the mathematical definition in the bracket.
WOW, great solution, I'll definitely implement it!
Thank You very much!
I implemented it, but I'm getting TLE which I shouldn't get because my solution uses O(NlogN) memory, right? Can You please view my submission 39701020?
You can use segment tree by sorting the queries in increasing R, the idea is same as Noam527 said.
Don't You know why I get TLE?
If You know/can know by viewing my code, please say me where's my mistake.