| # | User | Rating |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Why if xor sum of segment is equal to sum of segment, this condition is also satisfied for all subsegments of original segment?
I know that it's true when all bits in numbers are unique, but is it the only case when it's true, and if it is, then why?
Think about the binary representation of the bits. How is it possible that the xor sum is equal to the sum? If you figure that out, then it is obvious that this also holds for all subsegments.
My friend told me that it's satisfied when all bits are unique. Yes that makes sense and it's true. But is it the only case when xorsum is equal to sum?
Yes, of course. Assume that two numbers have the same bits set. Then in the xor sum these bits vaporize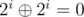
. And in the sum they add up 2i + 2i = 2i + 1. So if any bits are equal, then then the xor sum is guaranteed smaller than the sum.
Thank You very much, great explanation!
I'd also like to add that the there's a relation between the functions
sum&xor&andThat is sum(a, b) = xor(a, b) + 2 * and(a, b)
if looked closely at what Jakube said, if a = b then their
xorwould be 0 and all the bits that are both set (i.e. equals 1) in the binary representation ofa, bthat thexorfunction ignored because xor(1, 1) = 0 are accounted for by theandfunction because and(1, 1) = 1 and thus this value is shifted to the left by 1 bit (that is they get multiplied by 2)Hope this helps you visualize what's going on.
OMG, I'm blown away, thank You!
World of bits is so amazing!
You're welcome :)
Here's a practice problem for that 635C - XOR Equation
Thank You :)
is there any such relation for more than 2 numbers?
I guess it is easy to extend it, using bit manipulation. It's basically inclusion-exclusion.
We can see that $$$ sum(a,b,c) = xor(a,b,c) + 2*and(a,b) + 2*and(b,c) + 2*and(a,c) - 3*and(a,b,c) $$$
Because, if at a particular bit we have $$$0$$$ 1s or $$$1$$$ 1s, there is no problem, xor will cover that part of sum. When there are $$$2$$$ 1s in a particular bit, then xor will make it 0, so we need to add $$$2*and(a,b)$$$ for places that have bit in both $$$a$$$ and $$$b$$$, similarly other cases. Now, we see places where $$$a$$$, $$$b$$$ and $$$c$$$ all have bit set. Then, we have added that bit $$$6$$$ times, so we need to subtract $$$3$$$ of those.
UPD: The correct formula is $$$ sum(a,b,c) = xor(a,b,c) + 2*and(a,b) + 2*and(b,c) + 2*and(a,c) - 4*and(a,b,c) $$$
Look below for explanation and an example by Hossam
I think the last exclusion term should have a coefficient of 4.
for example:
$$$sum(1, 1, 1) = xor(1, 1, 1) + 2 * and(1, 1) + 2 * and(1, 1) + 2 * and(1, 1) - 4 * and(1, 1, 1) = 1 + 2 + 2 + 2 - 4 = 3$$$
You are correct, what I missed was that, xor will also add that bit one time. So need to subtract 4 times.
Auto comment: topic has been updated by prudent (previous revision, new revision, compare).