BledDest's blog

Разбор Educational Codeforces Round 46
By BledDest, 6 years ago, translation, In English

1000A - Codehorses T-shirts

Editorial
Solution

1000B - Light It Up

Editorial
Solution

1000C - Covered Points Count

Editorial
Solution

1000D - Yet Another Problem On a Subsequence

Editorial
Solution

1000E - We Need More Bosses

Editorial
Solution

1000F - One Occurrence

Editorial
Solution with persistent segment tree
Solution with persistent segment tree (a bit unreadable but runs faster)
Solution with standard segment tree
Mo-based solution

1000G - Two-Paths

Editorial
Solution
  • Vote: I like it
  • +53
  • Vote: I do not like it

Comments Comments (66)
| Write comment?
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can F be solved with a mergesort tree? ( By keeping all the elements which occur once in the nodes, where each node is a sorted vector. Also, merging is easy. )

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    How is merging easy? Sounds like at least O(n) if it's two pointers. Let the array be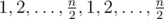 and all the queries are [1, n - 1]. How can you merge nodes fast enough?

    → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +6 Vote: I do not like it

    I used merge sort tree keeping for each element the range in which it's not repeated : My submission

    → Reply
  • »
    »
    4 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I used merge sort tree and passed with a time of $$$2901 \text{ ms}$$$, maybe should've used other method instead :/

    submission: Accepted

    → Reply
»
6 years ago, # |
  Vote: I like it +3 Vote: I do not like it

I like the fact that you have given different approaches for solving F. Thanks.

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

In B that's enough to check a_i + 1 only

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    You don't right.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Why not?

      → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 3   Vote: I like it 0 Vote: I do not like it

      hmm

      Am I wrong in the situaton when there are two adjacent points?

      I didn't think about it because my solution had AC

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
        ← Rev. 2   Vote: I like it +3 Vote: I do not like it

        Could you give a case please. Because if there are only 2 points the solution would be put nothing

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it +3 Vote: I do not like it

          No, I meant another thing. It's correct that making a point in a_i-1 and a_i+1 would give the same result. But sometimes it's impossible to put a point in a_i+1(like if there are points with coordinates x and x+1)

          → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 3   Vote: I like it +11 Vote: I do not like it

      There are some facts I can't prove because of my bad Englsh)) They are not very hard, but I can try to write proofs for them in Russian if you would want)

      It's enough. If we can put a point in ai + 1 and ai - 1, the result will be the same. So I can be wrong in a situation when we can put a point in ai - 1 but can't in ai + 1. Let's take a look at this. The points must be like ...ai - 1, ai, ai + 1(because we can't make a point at here)... Let's increase i until we find a free ai + 1. What do we get? A sequence of adjacent points. I want to say that the result will be the same if we put a point in the left of this sequence or in the right.

      If we don't find this i, it means there is a sequence with the end at M. in that case I say that the result will be the same if we put a point in the left or don't put at all.

      → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Mo-based solution for problem 1000F - One Occurrence is getting TLE

At first I try to write a solution with help of Mo-based solution Editorial, but I getting TLE, after getting many TLE I submit the code from Editorial exactly, but this also getting TLE...:(

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +26 Vote: I do not like it

    We never said Mo-based solution from the editorial gets AC. You still need to optimize things here and there.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +9 Vote: I do not like it

      See my submission using Mo's approach 39747523

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +5 Vote: I do not like it

        At last I get AC with a lot of change, but using Mo's approach. Here it is 39751860

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it +3 Vote: I do not like it

          i have a question with Mo's algorithm

          why use this cmp could get AC

          bool cmp(const Query &x, const Query &y){
	if(x.l/b == y.l/b) return (((x.l/b)&1)?x.r<y.r:x.r>y.r);
	else return (x.l/b<y.l/b);
}

          other cmp will get TLE

          → Reply
»
6 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Can anyone explain normal segment tree approach for 1000F - One Occurrence ?

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

What will happen in E if the graph is complete graph? there won't be any bridge. so what will be the answer?

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

The problem F is very similar to this problem from BZOJ.

Sorry for my poor English.

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can anyone elaborate 1000D.

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    dp[i] is the number of good sequences on the suffix from the i-th element.
    Then and dp[n + 1] = 1

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      please explain that logic with an appropriate example ...it'll be a great help :)

      → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it -8 Vote: I do not like it

      why are we multiplying with dp[j+1] int the above formula.

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it -8 Vote: I do not like it

        We can choose sequense of length a[i] whith start from i and finish to j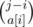 ways. After it you solve this problem on the suffix from j + 1 for other way of binom.

        → Reply
»
6 years ago, # |
  Vote: I like it -8 Vote: I do not like it

Mo-based solution of Problem F doesn't get AC.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Thanks for information! It is being discussed 3 comments higher.

    → Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Is it possible to use F's solution to query element that occurs exactly t times on a segment?

I think that in this case we would go with persistent ST from right to left (instead of left->right as in editorial). Suppose we are making a version that corresponds to l'th element of an array. We could precompute indices of occurrence of every array element. Suppose array[l] has more or equal than t - 1 occurrences after l: in this case we should update index of t - 1'th position with an index of t'th one or ∞ if such doesn't exist. So, the version l now contains t + 1'th occurrences of t'th elements. Initial version is initialized with negative infinities.

Now, the query [l, r] is the range maximum query [l, r] on l'th version.

As in editorial one needs to unset t + 1'th position assigning negative infinity to it.

I also realized that we could build the tree from left to right and do range minimum queries just as in editorial.

Please, tell me if there is an apparent flaw in this solution.

→ Reply
»
6 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Anyone please explain the solution of Problem 1000F with standard segment tree

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Why do we need to 'keep only the unique values' in the solution for problem C? I got AC with this and it was pretty straightforward.

→ Reply
»
6 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

I got it :) sorry for that comment

→ Reply
»
6 years ago, # |
  Vote: I like it +4 Vote: I do not like it

We can solve G online with same approach from editorial. Let f(2^i, u) is maximal profit of 2-path from u to 2^i th ancestor of u. f can easily calculated using d' and dp in editorial. Then, we can solve query (u, v) by binary jump on tree (similar to finding LCA).

Code: 39743132

→ Reply
»
6 years ago, # |
← Rev. 4   Vote: I like it 0 Vote: I do not like it

int tp = (i & 1) ^ 1; meaning in B solution code??Can anyone explain

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can anyone suggest a good resource for understanding and implementing bridges in a graph ?

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Is this some kind of hashing of edges? y = A[h] ^ B[h] ^ x; in Farhod's solution for 1000G.

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it -8 Vote: I do not like it

There's another way to do problem D that might make the code simplier. Maintain a dp[][] where the first dimension is the index you are at and the second dimension is the number of integers you have to choose to include before you can open another good sequence.

dp[i][k] is simply the sum of:

  1. dp[i — 1][k] (you didn't chose the current index to be included in the subsequence)
  2. dp[i — 1][k + 1] (you chose the current index to be included in the subsequence)
  3. dp[i — 1][0] if arr[i] = k and k isn't 0 (you open a new good sequence)

At the beginning, dp[0][0] = 1. At the end, the answer is dp[n][0] — 1 (because empty subsequence isn't allowed)

This is the code:

http://mirror.codeforces.com/contest/1000/submission/39787639

Opps and forget my dfs function it's not part of the solution.

→ Reply
»
6 years ago, # |
  Vote: I like it -8 Vote: I do not like it

My solution for Problem B — Light it up

https://coolforces.blogspot.com/2018/06/1000b-codeforces-light-it-up-solution.html

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

We don't necessarily have to answer the queries offline in 1000G.

→ Reply
»
6 years ago, # |
  Vote: I like it +11 Vote: I do not like it

Another cool dp for G: You can use the dp i -> i, and another one called "dpBestToRoot" which saves the best path to root (which is basically the best detour downward + the bestPathToRoot of your parent + the weight between you and your parent — your part in the detour of your parent).

Now you just do dpBestToRoot[u]+dpBestToRoot[v]-2*dpBestToRoot[lca]+dp[lca]. (http://mirror.codeforces.com/contest/1000/submission/39811424)

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I think more straightforward solution for G is to count dpv than build heavy light decomposition with prefix sums of ways where value for each node would be dpv - ev, u - max(dpu - 2 * ev, u) where v is node and u is child of v that lying on the same way(you know this ways in HLD) 39742958

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In fact, problem C can be solved with O(n) complexity,I think :P

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Anyone Plz HELP me for 1000C — Covered Points Count I am implementing the same logic as describes above but getting WA for Test Case 4 For Points Covered by 1 Segment. My Code — 39936831 THANKS IN ADVANCE

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In G, since wi > 0, does it matter if we remove the "twice" constraint in the statement?

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In problem E, what is being asked in the question and why the answer for that is equal to the diameter of the bridge tree instead of the total number of bridges?

→ Reply
  • »
    »
    4 years ago, # ^ |
    ← Rev. 2   Vote: I like it +5 Vote: I do not like it

    I also did not understand at the beginning. In the problem they ask to find two vertex such that the number of bridges between them is maximum The task does not give specific starting and finishing positions, you need to find such that the number of bridges between them is maximum (shortest path)

    → Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For problem F, I used a mergesort tree to get online queries in $$$O(\log^2 n)$$$ (barely snuck under the time limit).

Let each element in the array be a triple $$$(l, r, x)$$$, where $$$x$$$ is the value of that element, $$$l$$$ is the index of the previous occurrence of value $$$x$$$ in the array $$$+1$$$, and $$$r$$$ is the index of the next occurrence of value $$$x$$$ in the array $$$-1$$$. If there is no next or previous occurrence, then just use $$$+\infty$$$ or $$$-\infty$$$ or something.

Now, to query an interval $$$[a, b]$$$, we would like to know if there exists any triple $$$(l, r, x)$$$ in the array between indices $$$a$$$ and $$$b$$$, such that $$$l\leq a$$$ and $$$r\geq b$$$. If any such triple exists, we return $$$x$$$.

Now, we build a mergesort tree on the triples $$$(l, r, x)$$$ (sorted by $$$l$$$). Each node of the segment tree will store a sorted list of the triples on some interval, as well as a list of pairs $$$(r, x)$$$ which denote prefix maximums in terms of $$$r$$$ (and $$$x$$$ just gets copied over from whichever element had the largest $$$r$$$), on that sorted list.

Next, using normal segment tree tactics, we can make it so that for a query interval $$$[a, b]$$$, we only need to examine $$$O(\log n)$$$ nodes to try and find some valid $$$x$$$. For each node, we binary search the sorted list of triples to get a prefix such that $$$l\leq a$$$, and then take the corresponding $$$(r, x)$$$ at the end of that prefix, which gives us the largest possible $$$r$$$ on that prefix. If $$$r<b$$$, then no valid solution exists, otherwise the $$$x$$$ that we found is valid. Examining one node thus takes $$$O(\log n)$$$ time.

So, we can query an interval $$$[a, b]$$$ in $$$O(\log^2 n)$$$ time. Submission here: 84532864

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

strict time limit for problem F even edutorial solutions get TLE

→ Reply
»
16 months ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it
  • F can be solved with a simple minimum segment tree, a standard segtree + sorting technique.
  • We just require the last and 2nd last occurrence of each element to answer our queries.
  • In ascending order, we can sort queries (x, y) based on Y [end points].
  • We keep adding elements until we can answer a query. Let's call it an $$$ADD(value, index)$$$ operation.

  • To find the answer for each query, we can do a query on the segment tree, let's call it $$$FIND(l,r)$$$ operation, for the time being...

  • Now we will see how we can implement $$$add(v , i)$$$ and $$$find(l,r)$$$ functions using a segment tree.
  • add(value , i)
    • Change last occurence $$$i$$$ and second last occurence $$$j$$$ of $$$value$$$ accordingly.
    • set $$$segtree[i] = (j , val)$$$
    • set $$$segtree[j] = (inf , -1)$$$
  • find(l , r)
    • Lets do a min range query $$$(l , r)$$$.
    • If we get our pair as $$$(index, value)$$$ where $$$index < l$$$, then it means that the $$$value$$$ has one of its occurrences within range and its previous occurrence is outside the range. So $$$value$$$ is a perfect candidate for the answer.
    • If $$$index >= l$$$, then no such number exists with the unique occurrence, print 0.

Basic idea: Sort queries with endpoints, index segtree with last occurrence index, and find if any value's prev last occurrence is in out of range.
Code : https://mirror.codeforces.com/contest/1000/submission/214379121
Complexity: $$$O(NlogN)$$$

→ Reply
»
15 months ago, # |
  Vote: I like it 0 Vote: I do not like it

Problem G can be solved online in same complexity of $$$O((n + q)\log{n})$$$ with any tree path sum structure and some additional precomputation.

Implementation: link

→ Reply