Здравствуйте! Этот пост написан для всех тех, кто хочет освоить полиномиальные хэши и научиться применять их в решении различных задач. Я кратко приведу теоретический материал, рассмотрю особенности реализации и разберу некоторые задачи, среди них:
Поиск всех вхождений одной строки длины n в другую длины m за O(n + m)
Поиск наибольшей общей подстроки двух строк длин n и m (n ≥ m) за O((n + m·log(n))·log(m)) и O(n·log(m))
Нахождение лексикографически минимального циклического сдвига строки длины n за O(n·log(n))
Сортировка всех циклических сдвигов строки длины n в лексикографическом порядке за O(n·log(n)2)
Нахождение количества подпалиндромов строки длины n за O(n·log(n))
Количество подстрок строки длины n, являющихся циклическими сдвигами строки длины m за O((n + m)·log(n))
Количество суффиксов строки длины n, бесконечное расширение которых совпадает с бесконечным расширением всей строки за O(n·log(n)) (расширение — дублирование строки бесконечное число раз)
Наибольший общий префикс двух строк длины n с обменом двух произвольных символов одной строки местами за O(n·log(n))
Примечание 1. Не исключено, что некоторые задачи могут быть решены быстрее другими методами, например, сортировка циклических сдвигов — это в точности то, что происходит при построении суффиксного массива, искать все вхождения одной строки в другую и работать с собственными суффиксами позволят префикс-функция и алгоритм Кнута-Морриса-Пратта, а с подпалиндромами отлично справляется алгоритм Манакера
Примечание 2. В задачах выше приведена оценка, когда поиск хэша осуществляется при помощи сортировки и бинарного поиска. Если у Вас есть своя хэш-таблица с открытым перемешиванием или цепочками переполнения, то Вы — счастливчик, смело заменяйте бинарный поиск хэша на поиск в Вашей хэш-таблице, но не вздумайте использовать std::unordered_set, так как на практике поиск в std::unordered_set проигрывает сортировке и бинарному поиску в связи с тем, что эта штука подчиняется стандарту C++ и обязана много чего гарантировать пользователю, что полезно при промышленной разработке и, зачастую, бесполезно в олимпиадном программировании, поэтому сортировка и бинарный поиск для несложных структур одерживают абсолютное первенство в C++ по скорости работы, если не тянуть что-то свое.
Примечание 3. В тех случаях, когда сравнение элементов затратно (например, сравнение по хэшам за O(log(n))), то в худшем случае std::random_shuffle + std::sort всегда проигрывает std::stable_sort, так как std::stable_sort гарантирует минимальное число сравнений среди всех сортировок (основанных на сравнениях) для худшего случая.
Решение перечисленных задач будет приведено ниже, исходники тоже.
В качестве плюса полиномиального хэширования могу отметить, что зачастую не нужно думать, можно сразу брать и писать наивный алгоритм решения задачи и ускорять его полиномиальным хэшированием. Лично мне решения с полиномиальным хэшем приходят в голову в первую очередь, может поэтому я синий.
Среди минусов полиномиального хэширования: а) Слишком много операций остатка от деления, порой на грани TLE на больших задачах и б) на codeforces в программах на C++ зачастую маленькие гарантии от взлома из-за MinGW: std::random_device генерирует каждый раз одно и то же число, std::chrono::high_resolution_clock тикает в микросекундах вместо наносекунд. (Компилятор cygwin на windows лишен всех недостатков MinGW, в том числе и медленного ввода/вывода).
Что такое полиномиальный хэш?
Хэш-функция должна сопоставлять некоторому объекту некоторое число (его хэш) и обладать следующими свойствами:
Если два объекта совпадают, то их хэши равны.
Если два хэша равны, то объекты совпадают с большой вероятностью.
Коллизией называется очень неприятная ситуация равенства двух хэшей у несовпадающих объектов. В идеале, при выборе хэш-функции необходимо обеспечить как можно меньшую вероятность коллизии. На практике — такую вероятность, чтобы успешно пройти набор тестов к задаче.
Существует два подхода в выборе функции полиномиального хэша, которые зависят от направления: слева-направо и справа-налево. Для начала рассмотрим вариант слева-направо, а ниже, после описания проблем, которые возникают в связи с выбором первого варианта, рассмотрим второй.
Рассмотрим последовательность {a0, a1, ..., an - 1}. Под полиномиальным хэшем слева-направо для этой последовательности будем иметь в виду результат вычисления следующего выражения:

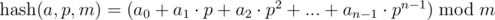
Здесь p и m — точка (или основание) и модуль хэширования соответственно.
Условия, которые мы наложим: 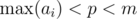 ,
, 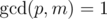 .
.
Примечание. Если подумать об интерпретации выражения, то мы сопоставляем последовательности {a0, a1, ..., an - 1} число длины n в системе счисления p и берем остаток от его деления на число m, или значение многочлена (n - 1)-й степени с коэффициентами ai в точке p по модулю m. О выборе p и m поговорим позже.
Примечание. Если значение 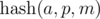 , не взятое по модулю, помещается в целочисленный тип данных (например, 64-битный тип), то можно каждой последовательности сопоставить это число. Тогда сравнение на больше / меньше / равно можно выполнять за O(1).
, не взятое по модулю, помещается в целочисленный тип данных (например, 64-битный тип), то можно каждой последовательности сопоставить это число. Тогда сравнение на больше / меньше / равно можно выполнять за O(1).
Сравнение на равенство за O(1)
Теперь ответим на вопрос, как сравнивать произвольные непрерывные подотрезки последовательности за O(1)? Покажем, что для их сравнения достаточно посчитать полиномиальный хэш на каждом префиксе исходной последовательности {a0, a1, ..., an - 1} .
Определим полиномиальный хэш на префиксе как:

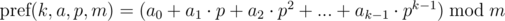
Кратко обозначим 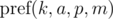 как
как 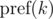 и будем иметь в виду, что итоговое значение берется по модулю m. Тогда:
и будем иметь в виду, что итоговое значение берется по модулю m. Тогда:

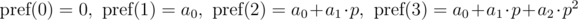
Общий вид:

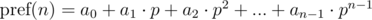
Полиномиальный хэш на каждом префиксе можно находить за O(n), используя рекуррентные соотношения:

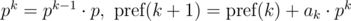
Допустим, нам нужно сравнить две подстроки, начинающиеся в позициях i и j и имеющие длину len, на равенство:

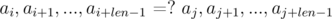
Рассмотрим разности 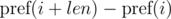 и
и 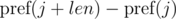 . Не трудно видеть, что:
. Не трудно видеть, что:

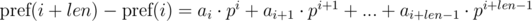
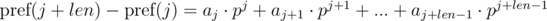
Домножим 1-е уравнение на pj, а 2-е на pi. Получим:

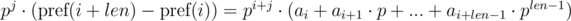
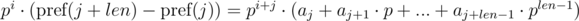
Видим, что в правой части выражений в скобках были получены полиномиальные хэши от подотрезков:

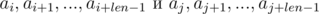
Таким образом, чтобы определить, совпали ли искомые подотрезки, необходимо проверить выполнение следующего равенства:

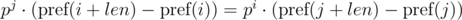
Одно такое сравнение можно выполнять за O(1), предподсчитав степени p по модулю. С учетом модуля m, имеем:

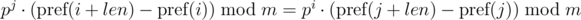
Проблема: сравнение одной строки зависит от параметров другой строки (от j).
Первое решение данной проблемы (предложил veschii_nevstrui) основывается на домножении первого уравнения на p - i, а второго на p - j. Тогда получим:

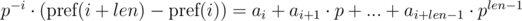
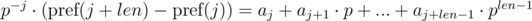
Можем заметить, что в правых частях был получен полиномиальный хэш от искомых подотрезков. Тогда, равенство проверяется следующим образом:

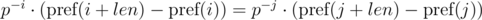
Для реализации этого необходимо найти обратный элемент для p по модулю m. Из условия gcd(p, m) = 1 обратный элемент всегда существует. Для этого необходимо вычислить значение функции Эйлера для выбранного модуля φ(m) и возвести p в степень φ(m) - 1. Если предподсчитать степени обратного элемента по выбранному модулю, то сравнение можно выполнять за O(1).
Второе решение данной проблемы основывается на знании максимальной длины сравниваемых строк. Обозначим максимальную длину сравниваемых строк как 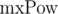 . Домножим 1-е уравнение на p в степени mxPow - i - len + 1, а 2-е на p в степени mxPow - j - len + 1. Тогда:
. Домножим 1-е уравнение на p в степени mxPow - i - len + 1, а 2-е на p в степени mxPow - j - len + 1. Тогда:

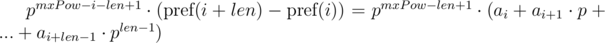

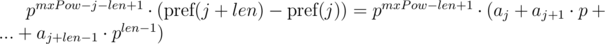
Можем заметить, что в правых частях был получен полиномиальный хэш от искомых подотрезков. Тогда, равенство проверяется следующим образом:

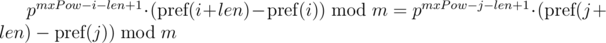
Этот подход позволяет сравнивать одну подстроку длины len со всеми подстроками длины len на равенство, в том числе, и подстроками другой строки, так как выражение 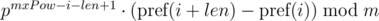 для подстроки длины len, начинающейся в позиции i, зависит только от параметров подстроки i, len и константы mxPow, а не от параметров другой подстроки.
для подстроки длины len, начинающейся в позиции i, зависит только от параметров подстроки i, len и константы mxPow, а не от параметров другой подстроки.
Теперь рассмотрим другой вариант выбора функции полиномиального хэширования. Определим полиномиальный хэш на префиксе как:

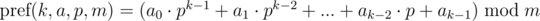
Кратко обозначим 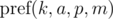 как
как 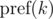 и будем иметь в виду, что итоговое значение берется по модулю m. Тогда:
и будем иметь в виду, что итоговое значение берется по модулю m. Тогда:

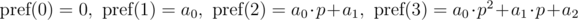
Полиномиальный хэш на каждом префиксе можно находить за O(n), используя рекуррентные соотношения:

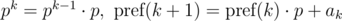
Допустим, нам нужно сравнить две подстроки, начинающиеся в позициях i и j и имеющие длину len, на равенство:

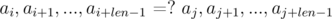
Рассмотрим выражение 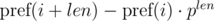 и
и 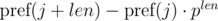 . Не трудно видеть, что:
. Не трудно видеть, что:

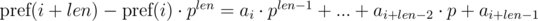
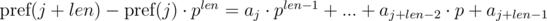
Видим, что в правой части выражений в скобках были получены полиномиальные хэши от подотрезков:

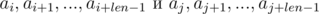
Таким образом, чтобы определить, совпали ли искомые подотрезки, необходимо проверить выполнение следующего равенства:

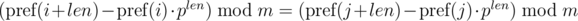
Одно такое сравнение можно выполнять за O(1), предподсчитав степени p по модулю m.
Сравнение на больше / меньше за O(log(n))
Рассмотрим две подстроки возможно разных строк длин len1 и len2, (len1 ≤ len2), начинающиеся в позициях i и j соответственно. Заметим, что отношение больше / меньше определяется первым несовпадающим символом в этих подстроках, а до позиции этого символа строки совпадают. Таким образом, необходимо найти позицию первого несовпадающего символа методом бинарного поиска, а затем сравнить найденные символы. Благодаря сравнению подстрок на равенство за O(1), можно решить задачу сравнения подстрок на больше / меньше за O(log(len1)):
Минимизация вероятности коллизии
Используя парадокс дней рождений, приведем (возможно, грубую) оценку вероятности коллизии. Пусть мы вычисляем полиномиальный хэш по модулю m и в ходе работы программы нам нужно сравнить n строк. Тогда вероятность того, что произойдет коллизия:

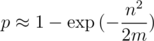
Отсюда очевидно, что m нужно брать значительно больше, чем n2. Тогда, аппроксимируя экспоненту рядом Тейлора, получаем вероятность коллизии на одном тесте:

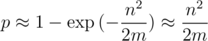
Если мы рассмотрим задачу о поиске вхождений всех циклических сдвигов одной строки в другую строку длин до 105, то мы можем получить 1015 сравнений строк.
Тогда, если мы возьмем простой модуль порядка 109, то мы не пройдем ни один из максимальных тестов.
Если мы возьмем модуль порядка 1018, то вероятность коллизии на одном тесте ≈ 0.001. Если максимальных тестов 100, то вероятность коллизии в одном из тестов ≈ 0.1, то есть 10%.
Если мы возьмем модуль порядка 1027, то на 100 максимальных тестах вероятность коллизии равна ≈ 10 - 10.
Вывод: чем больше модуль — тем больше вероятность пройти тест. Эта вероятность не учитывает взломы.
Двойной полиномиальный хэш
Разумеется, в реальных программах мы не можем брать модули порядка 1027. Как быть? На помощь приходит китайская теорема об остатках. Если мы возьмем два взаимно простых модуля m1 и m2, то кольцо остатков по модулю m = m1·m2 эквивалентно произведению колец по модулям m1 и m2, т.е. между ними существует взаимно однозначное соответствие, основанное на идемпотентах кольца вычетов по модулю m. Иными словами, если вычислять 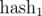 по модулю m1 и
по модулю m1 и 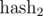 по модулю m2, а затем сравнивать два искомых подотрезка по
по модулю m2, а затем сравнивать два искомых подотрезка по 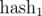 и
и 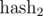 одновременно, то это эквивалентно сравнению полиномиальным хэшем по модулю m. Аналогично, можно брать три взаимно простых модуля m1, m2, m3.
одновременно, то это эквивалентно сравнению полиномиальным хэшем по модулю m. Аналогично, можно брать три взаимно простых модуля m1, m2, m3.
Особенности реализации
Итак, мы подошли к реализации описанного выше. Цель — минимум взятий остатка от деления, т.е. получить два умножения в 64-битном типе и одно взятие остатка от деления в 64-битном типе на одно вычисление двойного полиномиального хэша, при этом получить хэш по модулю порядка 10^27 и защитить код от взлома на codeforces.
Выбор модулей. Выгодно использовать двойной полиномиальный хэш по модулям m1 = 1000000123 и m2 = 2^64. Если Вам не нравится такой выбор m1, можете выбрать 1000000321, главное выбрать такое простое число, чтобы разность двух остатков лежала в пределах знакового 32-битного типа (int). Простое число брать удобнее, так как автоматически обеспечиваются условия gcd(m1, m2) = 1 и gcd(m1, p) = 1. Выбор в качестве m2 = 2^64 не случаен. Стандарт C++ гарантирует, что все вычисления в unsigned long long выполняются по модулю 2^64 автоматически. Отдельно модуль 2^64 брать нельзя, так как существует анти-хэш тест, который не зависит от выбора точки хэширования p. Модуль m1 необходимо задать как константу для ускорения взятия модуля (компилятор (не MinGW) оптимизирует, заменяя умножением и побитовым сдвигом).
Кодирование последовательности. Если дана последовательность символов, состоящая, например, из маленьких латинских букв, то можно ничего не кодировать, так как каждому символу уже соответствует его код. Если дана последовательность целых чисел разумной для представления в памяти длины, то можно собрать в один массив все встречающиеся числа, отсортировать, удалить повторы и сопоставить каждому числу в последовательности его порядковый номер в полученном упорядоченном множестве. Начинать нумерацию с нуля запрещено: все последовательности вида 0,0,0,..,0 разной длины будут иметь один и тот же полиномиальный хэш.
Выбор основания. В качестве основания p достаточно взять любое нечетное число, удовлетворяющее условию max(a[i]) < p < m1. (нечетное, потому что тогда gcd(p, 2^64) = 1). Если Вас могут взломать, то необходимо генерировать p случайным образом с каждым новым запуском программы, причем генерация при помощи std::srand(std::time(0)) и std::rand() не подходит, так как std::time(0) тикает очень медленно, а std::rand() не обеспечивает достаточной равномерности. Если компилятор НЕ MinGW (к сожалению, на codeforces установлен MinGW), то можно использовать std::random_device, std::mt19937, std::uniform_int_distribution<int> (в cygwin на windows и gnu gcc на linux данный набор обеспечивает почти абсолютную случайность). Если не повезло и Вас посадили на MinGW, то ничего не остается, как std::random_device заменить на std::chrono::high_resolution_clock и надеяться на лучшее (или есть способ достать какой-нибудь счетчик из процессора?). На MinGW этот таймер тикает в микросекундах, на cygwin и gnu gcc в наносекундах.
Гарантии от взлома. Нечетных чисел до модуля порядка 10^9 тоже порядка 10^9. Взломщику необходимо будет сгенерировать для каждого нечетного числа анти-хэш тест так, чтобы была коллизия в пространстве до 10^27, скомпоновать все тесты в один большой тест и сломать Вас. Это если использовать не MinGW на Windows. На MinGW таймер тикает, как уже говорилось, в микросекундах. Зная время запуска решения на сервере с точностью до секунд, можно для каждой из 10^6 микросекунд вычислить, какое случайное p сгенерировалось, и тогда вариантов в 1000 раз меньше. Если 10^9 это какая-то космическая величина, то 10^6 уже кажется не такой безопасной. При использовании std::time(0) всего 10^3 вариантов (миллисекунды) — можно ломать. В комментариях я видел, что гроссмейстеры умеют ломать полиномиальный хэш до 10^36.
Удобство в использовании. Удобно написать универсальный объект для полиномиального хэша и копировать его в ту задачу, где он может понадобиться. Лучше писать самостоятельно для своих нужд и целей в том стиле, в котором пишете Вы, чтобы разбираться в исходном коде при необходимости. Все задачи в этом посте решены при помощи копирования одного и того же объекта. Не исключено, что существуют специфические задачи, в которых это не сработает.
UPD: Для ускорения программ можно быстро вычислять остатки от делений на модули 231 - 1 и 261 - 1. Основная сложность заключается в умножении. Чтобы понять принцип, посмотрите следующий пост от dacin21 в параграфе Larger modulo и его комментарий с объяснениями.
Задача 1. Поиск всех вхождений одной строки длины n в другую длины m за O(n + m)
Дано: Две строки S и T длин до 50000. Вывести все позиции вхождения строки T в строку S. Индексация с нуля.
Пример: Ввод S = "ababbababa", T = "aba", вывод: 0 5 7.
Задача 2. Поиск наибольшей общей подстроки двух строк длин n и m (n ≥ m) за O((n + m·log(n))·log(m)) и O(n·log(m))
Дано: Длина строк N и две строки A и B длины до 100000. Вывести длину наибольшей общей подстроки.
Пример: Ввод: N = 28, A = "VOTEFORTHEGREATALBANIAFORYOU", B = "CHOOSETHEGREATALBANIANFUTURE", вывод: THEGREATALBANIA
Ссылка на задачу на acm.timus.ru с длиной до 10^5.
Ссылка на задачу на spoj.com с длиной до 10^6.
Задача 3. Нахождение лексикографически минимального циклического сдвига строки длины n за O(n·log(n))
Дано: Строка S длины до 10^5. Вывести минимальный лексикографически сдвиг строки A.
Пример: Ввод: "program", Вывод: "amprogr"
Задача 4. Сортировка всех циклических сдвигов строки длины n в лексикографическом порядке за O(n·log(n)2)
Дано: Строка S длины до 10^5. Вывести номер позиции исходного слова в отсортированном списке циклических сдвигов. Если таких позиций несколько, то следует вывести позицию с наименьшим номером. Во второй строке вывести последний столбец таблицы циклических сдвигов.
Пример: Ввод: "abraka", Вывод: "2 karaab"
Задача 5. Нахождение количества подпалиндромов строки длины n за O(n·log(n))
Дано: Строка S длины до 10^5. Вывести количество подпалиндромов строки.
Пример: Ввод: "ABACABADABACABA", Вывод: 32
Ссылка на задачу на acmp.ru с ограничениями до 10^5.
Ссылка на задачу на acmp.ru с ограничениями до 10^6.
Задача 6. Количество подстрок строки длины n, являющихся циклическими сдвигами строки длины m за O((n + m)·log(n))
Дано: Заданы две строки S и T длины до 10^5. Необходимо определить, сколько подстрок строки S являются циклическими сдвигами строки T.
Пример: Ввод: S = "aAaa8aaAa", T="aAa", Вывод: 4
Задача 7. Количество суффиксов строки длины n, бесконечное расширение которых совпадает с бесконечным расширением всей строки за O(n·log(n))
Дано: Строка S длины до 10^5. Бесконечным расширением строки назовем строку, полученную выписыванием исходной строки бесконечное число раз. Например, бесконечное расширение строки "abс" равно "abcabcabcabcabc...". Необходимо ответить на вопрос, сколько суффиксов исходной строки имеют такое же бесконечное расширение, какое и строка S.
Пример: На входе: S = "qqqq", на выходе 4.
Задача 8. Наибольший общий префикс двух строк длины n с обменом двух произвольных символов одной строки местами за O(n·log(n))
Дано: Строки S и T длиной до 2*10^5. Разрешается один раз обменять местами два произвольных символа строки S или не менять вовсе. Найти максимальную длину наибольшего общего префикса среди всех возможных замен.
Пример: На входе: S = "aaabaaaaaa" и T = "aaaaaaaaab", на выходе 10.
На этом все. Надеюсь, этот пост поможет Вам активно применять хэширование и решать более сложные задачи. Буду рад любым комментариям, исправлениям и предложениям. В ближайших планах перевести этот пост на английский язык, поэтому нужны ссылки, где эти задачи можно сдать на английском языке. Возможно, к тому времени Вы внесете существенные корректировки и дополнения в этот пост. Ребята из Индии говорят, что пытались сидеть с гугл-переводчиком и переводить с русского языка посты про полиномиальный хэш и у них это плохо вышло. Делитесь другими задачами и, возможно, их решениями, а также решениями указанных задач не через хэши. Спасибо за внимание!
Полезные ссылки:











Спасибо большое за туториал ! Очень полезно ! Буду с интересом разбирать !
Поступило предложение в качестве простого модуля использовать 2^31-1. Значения лежат в диапазоне [1 .. 2^31-1]. Смещенный остаток по этому модулю может быть вычислен без взятия остатка вообще вручную. Таким образом, можно добиться, что в полиномиальном хэше не будет ни одного взятия остатка. Как настроюсь — буду исправлять, поэтому не спешите.
Протестировано на задаче с подпалиндромами на acmp.ru длины до 10^6. Прошла только эта версия за время 1.8 секунд и памяти 31 МБ. Код.
UPD: код ниже работает, но не так, как вы ожидаете, он однозначно вычисляет смещенный остаток из диапазона
[1..2^31-1]вместо[0..2^31-2]от%.Да, вот быстрое взятие остатка по модулю
2^31-1без%. Сейчас объясню как это работает, но сначала более простой пример.Представим, например, число в десятичной системе счисления:
432. Оно запишется как:432 = 2 + 3*10 + 4*100. Допустим, мы хотим взять остаток от деления на9. Заметим, что:(2+3*10+4*100) % 9 = (2 + 3 + 4) % 9То есть, взятие остатка от деления числа в системе счисления с основанием
10по модулю9это сумма цифр, взятая по модулю9.Теперь наш случай. Рассмотрим наше число в системе счисления по основанию
2^31. Мы можем это сделать, так как все числа представлены в двоичной системе счисления. Теперь, если мы захотим вычислить остаток от деления на2^31-1— мы должны получить сумму цифр и взять ее по модулю, и т.д. пока не получили число, меньшее чем2^31-1.Итого, остаток от деления на
2^31-1 = 2147483647вычисляется следующим образом:Объясните, почему вы минусуете? Никогда не понимал, когда люди молча минусуют и ничего не пишут.
Протестировано на задаче с подпалиндромами на acmp.ru длины до 10^6. Прошла только эта версия за время 1.8 секунд и памяти 31 МБ. Код.
Хотя бы потому, что это не работает. Контрпример — 2147483647, и любое число, которое на него делится. А также число 9223372036854775807 = 263 - 1. Остаток должен быть равен 1, а получается равен 2147483648. Непорядок.
Ну и не совсем понятно, зачем в алгоритме складывать остаток от деления (x & 2147483647) и частное (x >> 31), хотя это чаще всего работает, но всё равно непонятно, как. (UPD. разобрался)
Разобрался, это работает немного по-другому, чем Вы ожидаете и я ожидал. Этот алгоритм любое ненулевое число до
(2^31-2)^2переводит в число из диапазона[1..2^31-1]однозначно. Этот алгоритм никогда не получит0в ответе. То есть, это смещенный остаток. Я думаю, если избавиться от нуля вообще, то для хэширования можно оставить, или я не прав?Я протестировал эту штуку на задаче с подпалиндромами длины 106 на медленном acmp.ru она прошла за время 1.8 и память 31 Мб. Остальные не прошли — TLE на 10-м. Код. По моим подсчетам, до 320 млн операций умножения 64-битных чисел и адресаций в памяти. Поэтому хэш без операций
%проходит.UPD: похоже, что нельзя прибавлять на входе 2^31-1, имейте в виду. Метод с прибавлением работает до чисел (231 - 2)2 + 231 - 2 — то, что нужно, так как одно умножение остатков и одно сложение остатков (Аналогия с 10-тичной с.с.:
109 % 9 = (10+9) % 9 = 10 % 9 = 1— требуется три шага). В таком случае, если избегать нулей в кодировании чисел, то нулевой хэш после вычитания получается только у строк нулевой длины.Awsome blog :D
Thanks, I not added problem from your contest, I'm sorry, I will add this
Added your problem and my solution as a Problem 8
feeling honoured(:p) after u mentioned our problem XD!!
Although while making the problem I was sure a solution with binary search exits for this problem but the closest we can get to a binary search solution was this : solution which is surely wrong (:p).
Now after learning rolling hash, will try to implement your solution :).
Please add a anti-hash test against single modulo 264 for your problem. Special generator for your problem. My old accepted solution with single hash gets wrong answer on this test.
UPD: added, now solution with 264 gets wrong answer
And in this problem it is necessary to generate more (maybe random) tests with length
200000and not-zero LCP, because single integer mod ~109 accepted. For example, in problem 6 46 tests, so solution with random single hash ~10^9 to this problem gets wrong answer.UPD: I generated 100000 random tests with length 200000 and no one collision for single modulo with random point.
Got your point..
Thanks a lot dmkz :)
В гарантиях от взлома, мне кажется, или надо смотреть не время отправки решения, а время запуска на сервере?
Исправил, спасибо
Can you please explain the method used in problem 3 with some examples and pseudo-code? I'm not able to understand the method of Comparison by greater / less in O(log(n)) time.
Let
S = 'aaaaab'Firstly we duplicate
Sand givenS = aaaaabaaaaab. We know that in this string cyclic shifts is:Suppose we need to compare
i = 0withi = 2inO(log(len))using binary search.I write substring as pair of position of start
iand length of substringlenbecause we can compare this pairs by equal inO(1)with polynomial hashes. I hope that this example can helpful for you to understand this techniqueЧто за ад с формулами? Это же невозможно читать :)
Я изначально написал в Markdown-разметке, но потом понял, что получается очень криво из-за многобуквенных обозначений, вроде pref и т.д, переделал с использованием вставок кода, показал двум знакомым, сказали, что читаемо. Сегодня понял, что можно было использовать \text{}. Нечитаемы только математические формулы? У меня была еще проблема, что формула, ограниченная двумя долларами, налезала на предыдущий текст, это фиксится?
UPD: Нашел костыль, кое-что изменил
Проверка на равенство за O(1). Мне кажется, что произвольные подпоследовательности нельзя просто так сравнить за O(1), потому что их нельзя получить за O(1). Подпоследовательность — это когда мы из строки выкидываем произвольные символы, а всё что осталось берём за нашу подпоследовательность. Т.е. символы не подряд в них идут.
По поводу минуса — можно первый хеш домножать не на pj, а на p - i. Соответственно, второй хеш домножать на p - j. Если наш модуль простой, то это сделать легко. И другой подход тогда будет не нужен.
UPD. Кстати, в другом подходе вы делаете то же самое, но зачем-то домножаете на ненужный коэффициент pmxPow - len + 1. Имхо, он не нужен, давайте убирать лишнее из красивых формул)
Спасибо за Ваш комментарий!
Вы правы, я исправлю на "непрерывный подотрезок" со следующей правкой.
Да, можно умножать на обратный элемент, тогда формулы становятся красивее, но это усложняет код, так как необходимо предподсчитать обратный элемент для основания в кольцах вычетов по модулям, которые мы используем, видимо, увеличится расход по памяти. Правильно ли я понимаю, что для этого нужно знать значение функции Эйлера от используемого модуля и возвести в степень φ(m) - 2? Например, φ(264) = 264 - 263 = 263, обратный элемент для нечетных чисел в 264 существует, все в порядке. Это увеличивает багаж того, что нужно знать, но как альтернативный вариант — рассмотреть можно. Лично я думаю, что вариант с доведением полиномиального хэша до фиксированной старшей степени предподчительнее.
Расход памяти это не увеличивает. Вы ведь предподсчитали степени числа p? И, если я не ошибаюсь, используете их только в этом месте? Давайте вместо них предподсчитаем обратные к этим степеням. Это довольно просто — находим p - 1, а потом просто возводим его в нужную степень: p - n = (p - 1)n. Расход памяти получился таким же.
Да, для этого нужно знать значения функции Эйлера. Но большинство людей использует простые модули, а для простых чисел эта функция довольно проста: φ(p) = p - 1. Только надо возводить в степень φ(n) - 1, но это мелочи. Для простых чисел знать теорему Эйлера не обязательно, достаточно малой теоремы Ферма.
В результате выполнения вашей функции, что у вас получается? Полиномиальный хеш, умноженный на какую-то константу. А у меня получается просто полиномиальный хеш, то есть в перспективе мой метод можно использовать лучше. Например, я без проблем могу найти хеш от конкатенации подстрок.
При описанном в статье подходе тоже можно конкатенировать две подстроки за два умножения (четыре, если хэш двойной полиномиальный). Допустим, необходимо выполнить конкатенации подстрок {i, n1} и {j, n2}, тогда:
.
Здесь $mxPow$ не превосходит удвоенной длины исходной строки.
У Вас, похоже, тоже 4 умножения:
Но тогда тоже нужно будет предподсчитывать положительные степени $p$, по памяти выйдет также.
UPD: Я внес правки в статью, добавив Ваш способ, спасибо
UPD2: Исправлена проблема со скобочным балансом в первом способе
У Вас проблемы со скобочным балансом. И с pi + n1 - j, i + n1 - j может быть отрицательным.
Но я имел в виду немного другое. Лично мне хочется какой-то инкапсуляции, так код будет легче понимать. То есть, например, я хочу отдельно функцию, которая выделяет мне хеш подстроки, и отдельно функцию, которая находит хеш конкатенации.
В первой функции у нас у обоих будет 1 умножение — мы оба домножаем хеш до некоторой « универсальной константы ». У меня это 1, у вас — pmxPow - len + 1.
Однако во второй у Вас уже начинаются некоторые неприятные вещи — необходимо домножить коэффициент у второй строки так, чтобы он стал равен pmxPow - len1 + 1 + len1 — чтобы можно было вынести pmxPow - len1 + 1 за скобку, а внутри получился нормальный хеш. То есть, домножить его на plen2. После этого можно спокойно сложить два хеша, но теперь надо привести их к оговорённому Вами виду, то есть у полученного хеша коэффициент должен быть равен pmxPow - len1 - len2 + 1. Сейчас он равен pmxPow - len1 + 1, то есть домножать на обратный элемент всё равно придётся.
Заметим, что мы коэффициент у хеша второй строки сначала умножили на plen2, а потом разделили на него же. То есть, справедливости ради, у Вас тоже можно обойтись одним умножением, но умножать придётся на p - len2, а Вы хотите этого избежать.
В моём же случае всё предельно просто — умножаем коэффициент у второй строки на plen1 и складываем получившиеся числа.
Исправлено, теперь нет отрицательных степеней и нет проблем со скобочным балансом. Я не вижу никаких проблем кроме как ошибиться в степенях. Если Вы захотите выполнить минимальное количество умножений, то в Вашем варианте тоже можно ошибиться в степенях. По поводу инкапсуляции: мы требуем, чтобы у результата вычисления полиномиального хэша была фиксированная старшая степень, мы задаем ту, которая нам нужна. Поэтому все инкапсулировано.
Если мы предподсчитаем хэш в обратном направлении, то обратные элементы не понадобятся:
Последовательность:
a[0], a[1], a[2], a[3], ..., a[n-1]Хэш на префиксе:
Или через рекуррентное соотношение:
Хэш вычисляется так:
Например,
hash(3, 3):Тогда сравнивать по хэшам красиво и коротко можно так:
Так как у хэша при таком вычислении фиксированная нулевая степень как универсальная константа.
Не смотря на красоту, такой хэш сложно изменять. Для хэша слева-направо при замене одного символа достаточно увеличить / уменьшить значения на суффиксе — с этим справится двойной Фенвик или одно дерево отрезков. Для хэша справа-налево нужно что-то похитрее на префиксе.
Может быть Вы знаете как поддерживать динамический хэш в таком случае за
O(log(n))?UPD: придумал, как это сделать деревом отрезков
Не увидел коммент выше в спойлере
Вы раньше писали о сокращении количества умножений. Могу ошибаться, но я посчитал, что количество умножений столько же при хэшировании справа-налево. Если при доведении до старшей степени 2 умножения на каждый хэш, то здесь умножение происходит при вычитании
pref[pos]. Как мы можем сократить количество умножений?This question : QQ is same as problem 2. But here i'm getting TLE. Submission. Any suggestions?
Solution has
10^6*log2(10^6)^2 ~=~ 4*10^8operaions in worst case, no way gets accepted withstd::map.For example, it is slower then
std::sort + std::binary_search6 times. Bench:You need to write your own hashtable to getting
O(n*log(n))solution withO(1)time per searchActually it will depend on the range of elements of the array.
(Assuming the number are uniformly distributed in the array).
Let say size of array is N = 1e6 and range of elements is 1 to 1e9, then surely sort + binary_search is a better option.
But if N = 1e6 and range of elements is 1 to 1e4 than std::map will beat sort + binary_search.
I still think that sort + unique + binary search will beat std::map. Do you have any experiment?
Oh! by adding unique I can accept it.
Note that we are very close in time. We can solve this problem if we introduce new symbols of fixed width. Note that each character can take four different values. We can combine adjacent characters and encode them as one. For example, if we combine four characters, we will make
4 * 4 * 4 * 4 = 256different combinations. We will convert the string in this way and find the maximum length in this case. Let this bemax1. Then we convert back and look for4 * max1to4 * max1 + 7.UPD: This improvement led to a solution in
O(n log(n)^2)with smaller constant. Accepted on SPOJ, code. On ideone.com0.83stime (just uncomment gen in line 148 for getting it)Can you help me with this problem ?
Given a string s of length <= 10^5 , given Q <= 10^5 queries , in each query you will be given L and R , you need to count number of sub strings of the string from L to R which are palindrome !
I know the hash based approach for finding the no of palindromic sub-strings in a given string.But I am not able to think how to extend the logic for handling range queries.
Can you help me with this problem ?
Given a string s of length <= 10^5 and Q <= 10^5 queries , In each query you have to consider a sub-string from index L to R and print number of palindromic sub-strings of the query string .
I know the hash based approach for finding the number of palindromic sub-strings of a given string but I am not able to extend the logic for handling queries .
I think that it can be solved with palindromic tree. Maybe with hashes too, but I don't know how.
Yes It can be solved using that also but I think there exist a solution which is hash based and make use of bit/ segment tree for handling range queries.It will be a great help if you can tell me that solution
I have an offline solution in O(n * log(n) + q * log(n)).
Pass i in decreasing order. Let k be the longest odd palindrome with center on i computed as problem 5. On a segment tree add 1 on every position on range [i-k+1, i]. Do the same for even length palindromes(center on i and i+1). Then we can answer a query [L, R] such that L = i by doing range sum query on the segment tree on range [L, R].
Please tell in more detail how you will answer on query?
I think the complexity of problem 2 is O((n + m * log(n)) * log(m))
Changed, thanks
I think you have to change it also in a russian version.
Actually, I believe that we could reach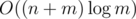 asymptotics with hashtable (but not STL version, it's kinda slow). As far as I remember I had something like 3-4 times boost (maybe even more) with hashtable.
asymptotics with hashtable (but not STL version, it's kinda slow). As far as I remember I had something like 3-4 times boost (maybe even more) with hashtable.
Can you, please, solve this problem with hashtable? I tried, but my hash table did not win against a accepted binary search
Well, I have two different variants of hashtables (with separate chaining and open adressing). Both got AC, but actually I needed to make some fixes because of size (first, I forgot about alphabet, then I forgot about size). But after this fixing separate chaining hashtable was good. Open adressing hashtable had some troubles with time before I changed the size of table up to 4·106 + 37. Finally I have 22ms (I hope it is ms) with open adressing hashtable and up to 15.97ms (with some experiments, my first result was 17.31ms) with separate chaining one.
I don't think that my hashtable is the fastest in the world, but here is my old-but-gold code, maybe you are interested: https://ideone.com/hxlvr0
UPD: I also have TL with binary search, so I think I can improve my code performance by changing the algorithm of string hashing.
I passed the solution with binary search only after I reduced the hidden constant, compressing four characters into one. More in this comment
I think that time in seconds — time of working on all test cases summary. For example, my binary search solution gets 19.19 time on SPOJ.
Your solution takes 0.8 seconds on ideone.com on test
10^6len, this is very fast hashtable, thanks! My solution with hashtable on this test takes 2.5 seconds, with binary search 1.6 seconds, with compressing 4 chars to 1 and binary search 0.66 seconds.Maybe your implementation of hashtable uses something like
vector<vector<...> >that can slow down solution because of memory allocations/deallocations.My implementation uses something like linked lists stored in continuous section of memory without changing the size so it could allocate it once and then just reuse it.
Thanks! I passed a problem with my open addressed hash table based on
std::array. Code.Now you can change the asymptotics of the problem 2 :)
Added rolling hash right-to-left and code for fast multiplication of remainders modulo 261 - 1 with link to the author
Добавлен полиномиальный хэш справа-налево и код для быстрого вычисления остатка по модулю 261 - 1 после умножения двух остатков со ссылкой на автора
Hi @dmkozyrev
In the second solution for rolling hash. You have mentioned that on both sides we need to multiply by MaxPow — i — len + 1. Do you think we can skip even len also, and make it MaxPow — i + 1 ? Because anyhow if both the substrings are of same len, we can check the equality without len also.
Yes, your approach — fixing least power of base in hash, and it's working
".. we take a module of the order 10^18, then the probability of collision on one test is ≈ 0.001. If the maximum tests are 100, the probability of collision in one of the tests is ≈ 0.1, that is 10%."
If the probability of collision on one test is 0.001, isn't the probability of at least one collision in 100 tests = 1 — (0.999)^100 ?
I used Taylor Series. When $$$n$$$ is large, but $$$p$$$ is small, we can just multiply $$$p$$$ by $$$n$$$:
Lets calculate original formula in wolfram:
From Taylor approximation we got:
Got it, thanks!
How Can I Find The the Kth Lexicographical Minimum Substring of a given string S ??
Please help....
Решение для 5-ой задачи с ограничением до 10^6 получает TL на 10 тесте. Моё решение получает ML на том же тесте. Может когда-то оно и работало но сейчас тесты изменили. Возможно ли теперь с такими тестами решить задачу с помощью хэшей?
Сдал одинарным хешем по модулю
2^61-1. Теория по взятию остатка от деления на2^p-1тутImages disappear now
:( for a while, I was solving this task and the images were not loaded i thought it was my network problem but now I understand that it is something wrong with the website. Still Solved it using pen and paper ;)
It is fixed
Thanks for the informative post. Regarding the definition of $$$hash(a,p,m)$$$, I can see why we make the assumptions:
However, what is the reason for assuming $$$p<m$$$?
If $$$p = m$$$, then hash is equal to value of $$$a_0$$$. If $$$p = m+1$$$, then hash is equal to $$$a_0 + a_1 + ... + a_{n-1}$$$. If $$$p = m + k$$$, then $$$p = k \text{ mod } m$$$. So, we can use just $$$p < m$$$ and it will be as good as $$$p = m + k > m$$$.
Nifty, thanks for explaining!
dmkz great-great tutorial, thx :)
I don't really get the part with collision probability estimation. Can anyone suggest some literature?
dmkz доброго времени суток! Можешь объяснить чем плох подход "cправа-налево"? Выглядит проще чем "cлева-направо", но при этом активно юзается последний.
Можно и справа-налево использовать, тут дело вкуса. Справа-налево, вроде, даже удобнее в Дереве Отрезков поддерживать, если есть запросы на замены символов в строке.
Понял. Благодарю за отличную статью!
Thansk bro very very much, I was looking for such a hashing tutorial.
I was solving this problem using hashing but hash was not good enough, but after reading this tutorial I was finally able to solve it.
I have a slightly more optimized version of the $$$2^{61}-1$$$ modulus multiplication:
note 1: Karatsuba's technique, saving one multiplication at the cost of three additive operations
note 2: get low 61 bits of product
note 3: add high 61 bits of product. Small adaptation of the classic multiplyHigh algorithm. Also add the +1 fudge factor to help reduction
note 4: only one reduction needed, as high 61 bits can't be all ones
Sorry for necroposting but actually for the problem Lexicographically Minimal String Rotation, I actually found a way myself to only need $$$O(n \log \log n)$$$ complexity, I called it as Logarithm Decomposition. But for this the LMSR problem, I still think $$$O(n)$$$ Lyndon-Duval Algorithm and my $$$O(n)$$$ Subaru Trick is simple and fast to be coded.
I tried to research the problem for few days and still not know whether or not the hashing only by itself can be used to solve the LMSR problem in $$$O(n \log \log \log n)$$$ or similar. (What I mean is that if I apply Hash to any of my 3 solutions $$$O(n \log n)$$$ Subaru Trick then it will be $$$O(n)$$$ but the constant is high enough that is just not even worth it)