Здравствуйте! Пытаюсь сдать задачу "882. Губернатор" с сайта acmp.ru. Недавно я создавал аналогичный пост для другой задачи, под которым подсказали, что в задачах такого рода должен работать жадный алгоритм и нужно лишь определить предикат для сортировки.
В этой же задаче я понял, что ответ не зависит от K и необходимо минимизировать сумму: 
Здесь индексами обозначена последовательность взятия.
Я генерировал маленькие случайные тесты, для которых можно перебрать все n! перестановок и пробовал подобрать предикат, но все безрезультатно. Максимально близко к случайным тестам размера 10 подошел предикат 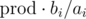 , где
, где 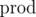 — произведение всех ai. На этом идеи кончились и нужна помощь. Может из-за маленького n решение предполагает динамику за O(n2) времени с памятью O(n), но с ней тоже не вяжется.
— произведение всех ai. На этом идеи кончились и нужна помощь. Может из-за маленького n решение предполагает динамику за O(n2) времени с памятью O(n), но с ней тоже не вяжется.










Сортируй типа есть пары ai,bi и aj,bj тогда первую лучше раньше брать если aibj+bi<ajbi+ai
К сожалению, не взлетело
Единственная правильная последовательность это:
6 5 8 3 7 2 9 1 10 4При такой сортировке получается:
6 1 5 8 3 2 7 9 10 4Код
Туплю немного , хотел написать aibj+bi<ajbi+bj
Да, я исправил опечатку и у Вас, и у меня. Я обновил контр-пример.
Там ожидается сортировка с предикатом (ai - 1) / bi > (aj - 1) / bj.
Честно говоря, я сам был бы очень признателен, если бы кто-нибудь объяснил, как и почему это работает.
Спасибо, зашло, ниже написали объяснения
Предположим, что ai = 1 нет, вернемся к ним позже.
Посмотрим, при каком условии будет выгодно поменять соседние элементы (a1, b1) и (a2, b2). Для этого нужно сравнить b1·a2 + b2 с b2·a1 + b1, то есть b1·(a2 - 1) с b2·(a1 - 1). Если a по разные стороны от единицы, то раньше должна идти та, что больше единицы. Другими словами, в оптимальном решении сначала идут все пары с ai больше единицы. Если a по одному сторону от единицы, то можно все разнести по разные стороны неравенства и получить валидный компаратор.
Теперь выясняется, что нам повезло, и наибольший префиксный максимум по произведению ai-х образуется всеми ai-ми большими единицы. Поэтому элементы с ai можно засунуть после них в любом порядке.
Спасибо! Если рассмотреть следующий компаратор:
То он проходит. Есть ли против него контр-тест?
Почти любой рандомный тест должен подойти (даже если не обращать внимание на деление на 0).
К сожалению, контр-тест не был обнаружен после генерации 10000 рандомных тестов на 1000 элементов. Код
Компаратор, который вы написали в прошлом комментарии не проходит (по ссылке в коде компаратор другой). По ссылке на самом деле компаратор правильный, потому что bi положительные и можно без каких-либо дополнительных предположений поделить на них обе части (в моем описании я не учел, что bi строго положительные и слегка перемудрил).
Очень странный факт: результаты работы двух этих методов различны на 8-м тесте на acmp.ru. Я составил решение, в котором вызываются оба метода, а затем сравниваются по сумме с точностью до 1e-18L. Код. Срабатывает assert при сравнении по сумме. Тем не менее, проходят оба метода.