Given T test cases T<=100000 In each test case given a positive integer A.A<=100000 You can perform any of the following steps(one of them):.
1) decrement A by 1.
2) increment A by 1.
3) divide A by one of it's prime factor.
Find minimum number of steps to reduce A to 1. 1) it is best to divide by max prime factor or finding nearest prime number whichever is minimum. This is codeforces problem but I can't find it











Constraints of A?
same as T, i.e. A<=100000
if increment by 1 step would not be there then it can be done in aloga time..by maintaining the lowest prime divisor for each numbers(1->a) using seive then maintaining the answer(dynamic programming) array of size (a+1) using indices (1->a), ans[1]=0 and ans[i] can be calculated by min(ans[i-1],min(ans[i/p] for all prime divisors of i )) + 1. prime divisors for a particular number 'n' can be found in logn time hence it is (seive + aloga).. pls somebody explain how to do this with increment operation also
Basically you can return 1 for each prime number and the prime gap at most can be around 100 so algo:
Int solve(a){ If(a==1). Return 0;
If(isprime[a]) return 1;
Return min(solve (a-1),solve(a+1),solve(a/x)); // for all x which is prime divisor of a using seive).
}
And use memoization
This problem can be solved with Dijkstra. We extend the directed edge from x+1 to x and from x-1 to x. (1 <= x <= 100010) For the prime factor p of x, we extend the directed edge from x/p to x. You can use Dijkstra to find the distance from 1 to A_i. The solution is like this. The time complexity is
I suppose that the number of edges is NlogN, but in fact, it is 377926 when N = 100010, so it may be considered that the time complexity is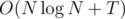 .
.
Yeah, but will not a recursion with memoization work? I think won't , because prime gap is around 100
Before that, did you investigate how your own solution works? I have not seen your code. Since solve (x) calls solve (x + 1) and solve (x + 1) calls solve (x), will not we get out of this infinite loop? If you want to search on this problem, it is bfs from x = 1, not dfs from x = a. I used dijkstra, but if you do a normal bfs you can get an answer in linear time.
yeah got it ,thanks
Using BFS instead of dijkstra could improve the solution.
yes as all steps are same
build a graph and find the shortest path to reach from node A to node 1 using the Dijkstra algorithm.
Your solution will definitely get TLE. The time complexity is O (TNlogN).
but his solution is exactly your solution...
Completely different
How?
Because Reina_Kousaka's solution builds the shortest path tree from node 1, which allows you to answer queries for every node once the Dijkstra is done.
Meanwhile, constructing a graph from node A only solves the question for that node.
thank you, oreki-san
Yes,dijkstra will do it because we have to find all nodes shortest path