Thanks to Gassa and the other organizers for the very nice contest. I hope for more marathon contests to be organized in the future.

My solution is indeed based on beam search. The code of my final submissions is available here : https://0bin.net/paste/iruL7y-FkxFbUXe3#PyLGLPPBXS2BzXB8b3GVJjMnf7WTVq0AjToA9srxmQG. (The important part starts on line 944). Thanks to the writers of https://probablydance.com/2016/12/02/investigating-radix-sort/ and https://stackoverflow.com/a/36205084 for their sorting functions that I used for performance reasons.

The states of the beam search are the chameleon positions and the colors of the bottles in the hand. I consider at each step all possible moves for all chameleons.

Here are the main components that made my approach work :

• Avoid keeping similar states : Beam Search offers little improvement over a greedy algorithm if several equal states are kept (which can happen when independent, commuting moves are possible). For this particular problem, I chose to ignore a state whenever a state with the same hand colors and better sorted chameleon positions had already been considered (lines 1109-1116).

• Use a good scoring function : At the end, we want to optimize the minimum chameleon position, but this is not a very good scoring function to optimize during the beam search. I tried several different scoring functions to sort the states of the beam search, and ended up with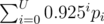 , where (p_i) is the sorted list of the chameleons' positions (line 1083). It is probably possible to improve it, by considering for instance the colors of the squares under the chameleons, and the colors of the bottles in hand. It however has the advantage of being rather cheap to compute.

• Optimize the program and increase the beam width : By doubling the beam width of my last submission, the scores obtained by my code can still increase by more than 500 points. Any small optimization that allows submissions using a larger beam width to fit in the time limit is reflected in the score.

Well the contest was really amazing, I tried many ways and finally my rank was only 62 (not good enough :( ).
But i had no clue as to what beam search was! Well thanks to the editors and other participants who introduced this topic hope i will find this useful!
Anyways i will state the few methods that i tried!
1) I initially i also used the sol. NO. 1 in the blog and got 9k points
2) Then i tried to play with random numbers i would randomly select a chameleon and a random color in the hand.(This didn't get me anywhere worse than method 1 :p)
3) Then i wrote the greedy solution which got me the 32096 points.
4) Fourth time what i did was that would select the last 5 chameleons and try all permutations of sending these 5 chameleons one by one to the best location greedily and among all permutations i would select the best and then would update the positions and then i would repeat the process (This gave me the best score 33285.278). I also tried taking last 6 but that would give a TLE so i tried skipping some permutations but that did not help!

Anyways it was fun and kept me engaged for a while and i would to attend more such marathons!

Thank You Gassa, naagi, KOTEHOK for this contest!

I'm very surprised that the top solutions are essentially just smart brute-force.

I personally tried a lot to optimize the greedy algorithm with heuristics.

Initial greedy: If a chameleon can't catch up to any chameleon, throw the best bottle at it (so nobody gets left behind). Otherwise, pick the chameleon-color combination that goes the furthest, and use that. I found this was better than always throwing it at the last one, though i had some bugs in my solution early on so I'm not sure :P

Then, later, instead of just calculating the chameleon that went furthest, I tried to add a number of heuristics, such as

• If a chameleon is standing in a useful spot — that is, it is standing on a square of color C, the next square of color C is pretty far away, there are chameleons behind that chameleon, and you are holding bottle(s) of color C, then decrease the priority of throwing a bottle at that chameleon.

• If throwing a bottle of color C at a chameleon would put it in a useful spot (useful means as above), then increase the priority of throwing a bottle of color C at that chameleon.

Ultimately, though, these heuristics barely made it better than the greedy solution.

I'm wondering if anyone managed to improve the greedy solution by a lot using some similar heuristics.

it makes me think of alpha go and reinforcement learning, where you use some kinds of expansion at the end to estimate the current state...

когда будет системное тестирование?

Thanks all for designing the problems. Here are some thoughts during the week. I don't know about beam search so I mainly brute force all choices.

1) Choose the colour appears most in hand, and keep throwing to the last chameleon If that colour appears a lot in hand , then probably the chameleon can skip a lot since the next few locations of that colour are occupied.
Result : ~20k

2) Brute force on current step and choose the greatest move. However some chameleon moves a lot but some didn't. Possibly the 10 chameleon are divided into several groups at the beginning sincetheir relative position are not considered and one group lag behind.
Some chameleons at ~10k and some at ~30k
Result : ~10k

3) Taking both the number of squares moved and their relative position as consideration, movement - dist(Chameleon, Last Chameleon)
Result : ~33k , time <0.1s

4) Looking at (k + 1)^th step when deciding the (k)^th step. Brute force on all possible choices. I take the average of best few cases on (k + 1)^th step instead of the best to prevent some extreme cases. Adjust weightings between current step and next step. Get the best choice and move a step.
Result : ~34k , time 2~3s

5) Repeating (4) on (k + 2)^th step with some methods tried to reduce time:
- Not searching all choices on k + 2 step, but the last few chameleons.
- Ignore chameleons far away from the last one, say by 50 squares.
And finally try different values for parameters, such as:
- weighting of movement - dist(Chameleon, Last Chameleon) dependent on step
- weighting between current step and next steps
- non-linear measure for dist(Chameleon, Last Chameleon)
Result : 35.7k , time ~10s
However I don't know how they works. Also small improvement can be done if I can remove some possible choices at a earlier stage and search deeper.

Final submission: https://github.com/kmyiu/Codeforces_Marathon_R2/blob/master/cf_marathon.cpp