Существует ли полиномиальный (возможно, субоптимальный) алгоритм для нахождения остовного дерева с минимальным числом поворотов, на графе, представляющем из себя связное подмножество клеток грида (возможно, невыпуклое и с дырками).
Поворотом называется пара ребер, имеющих общий конец и направленных перпендикулярно по отношению друг к другу.
Например, на картинке ниже с гридом 4 x 4 (в данном случае прямоугольном, но может иметь любую форму, если рассматривать только подмножество клеток грида) остовное дерева справа (6 поворотов) лучше, чем остовное дерево слева (15 поворотов) 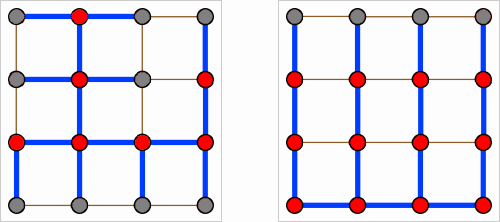











I think the spanning tree like one that on the right is always optimal
But cells in the grid form not always a rectangle. For example, for Г-shaped set of cells the optimal tree is
г------------------
г------------------
гттт--------------
||||||
||||||
||||||
||||||
H-shaped grid is more difficult
But that's not a grid graph?
Subset of cells in grid?
Auto comment: topic has been updated by shaviava (previous revision, new revision, compare).
approximation algorith: first make vertical, after that horizontal edges and merge with dsu just like kruskal's.
The expanded problem of this problem has already been taken here and can be solved using the Kruskal method.There is editorial on the link.(It is considered only when it is a rectangle) Even when it is not a rectangle, I think that it can be solved by the usual Kruskal method by setting the cost of the edge between adjacent vertices to 1.
There was a simple mst, but I want to minimize numbers of turns. And I can't reformulate this problem in terms of problem from atcoder
Но ведь слева 15 поворотов.
Ну хорошо, 15