I'm trying to come up with a recursive solution for this problem but I haven't been able to so far. Any advice/pointers here?
I tried 0-1 knapsack style but there is an issue with backtracking the array.
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 156 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |

I'm trying to come up with a recursive solution for this problem but I haven't been able to so far. Any advice/pointers here?
I tried 0-1 knapsack style but there is an issue with backtracking the array.
| Название |
|---|



It appears that the statement is actually asking for the number of permutations of 1... n with k inversions. If In(t) is the number of permutations of size n with t inversions, then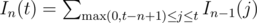 . This recurrence can be calculated in O(nt) using prefix sums on In.
. This recurrence can be calculated in O(nt) using prefix sums on In.