Vesper_Lynd's blog

how greedy approach worked in this problem?
By Vesper_Lynd, history, 6 years ago, In English

Source of problem I mean how greedy approach using recursion worked in this problem. Because lets say if for a particular value more than one pegs accept that value, than choosing the first one would give the best result how it can happen i mean, if we choose the later peg than it may happen that more balls can be put into, some solutions have greedy approach accepted,Please guide over here!! Uva 10276.

  • Vote: I like it
  • +1
  • Vote: I do not like it

»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by Vesper_Lynd (previous revision, new revision, compare).

→ Reply
»
6 years ago, # |
  Vote: I like it +2 Vote: I do not like it

Let f(n) denote the maximum number of balls one can place on n pegs.

Lemma 1: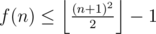 for all n.

Suppose n = 2k first and consider placing the 2k balls 2k2 + a where 0 ≤ a ≤ 2k - 1. It holds 2k2 + a + 2k2 + a + 1 > (2k)2, so the next ball must make a perfect square  ≥ (2k + 1)2 on each peg. It must at least (2k + 1)2 - (2k2 + a) > 2k2 + 2k + 1. That's impossible, because one cannot place 2k2 + 2k. Conclude that f(2k) ≤ 2k2 + 2k - 1. I leave the n = 2k + 1 case to you.

Lemma 2: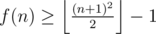 for all n.

Let g(n) be the number of balls placed by the greedy algorithm on n pegs. Use induction to show the greedy algorithm places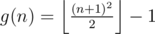 balls such that the n topmost balls form a permutation of g(n), g(n - 1), ..., g(n) - n + 1. This obviously holds for n = 1. If n ≥ 2, the greedy algorithm starts placing g(n - 1) balls on the first n - 1 pegs before peg n is used. Suppose n = 2k. By induction, we know that 2k2 - 1 balls are placed at this point with 2k2 - 1 - a being on the top for 0 ≤ a ≤ 2k - 2. Ball 2k2 can only be placed on peg n, since (2k - 1)2 < 2k2 + 2k2 - 1 - a < (2k)2. The algorithm continues placing 2k2 + 1 + a on the peg with topmost ball 2k2 - 1 - a for 0 ≤ a ≤ 2k - 2 and finally, 2k2 + 2k - 1 balls are placed with the topmost balls forming the desired permutation. The n = 2k + 1 case works quite similar and is left as an exercise.

Combining Lemma 1 and 2, we get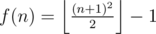 and the greedy algorithm provides a sufficient construction.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    thnx for explaining but one question,how you came up with that inequalities??

    → Reply