Разбор Educational Codeforces Round 49

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

Разбор

Решение (PikMike)

#include <bits/stdc++.h>

#define forn(i, n) for (int i = 0; i < int(n); i++)

using namespace std;


int main() {
    int T;
    cin >> T;
    
    int n;
    string s;
    forn(_, T){
        cin >> n >> s;
        bool ok = true;
        forn(i, n){
            int k = abs(s[i] - s[n - i - 1]);
            if (k > 2 || k % 2 == 1){
                ok = false;
                break;
            }
        }
        cout << (ok ? "YES" : "NO") << endl;
    }
    return 0;
}

1027B - Числа на шахматной доске

Разбор

Решение (Vovuh)

import sys

lst = sys.stdin.readlines()
n, q = map(int, lst[0].split())

for i in range(q):
    x, y = map(int, lst[i + 1].split())
    cnt = (x - 1) * n + y
    ans = (cnt + 1) // 2
    if ((x + y) % 2 == 1): ans += (n * n + 1) // 2
    sys.stdout.write(str(ans) + '\n')

1027C - Прямоугольник минимальной стоимости

Разбор

Решение (PikMike)

#include <bits/stdc++.h>

#define forn(i, n) for (int i = 0; i < int(n); i++)

typedef long long li;

using namespace std;

const int N = 1000 * 1000 + 13;

int n, m;
int a[N];
int b[N];

int main() {
    int T;
    scanf("%d", &T);
    forn(_, T){
        scanf("%d", &n);
        forn(i, n)
            scanf("%d", &a[i]);
        sort(a, a + n);
    
        m = 0;
        forn(i, n - 1){
            if (a[i] == a[i + 1]){
                b[m++] = a[i];
                ++i;
            }
        }
    
        int A = b[0], B = b[1];
        li P2 = (A + B) * li(A + B);
        li S = A * li(B);
    
        forn(i, m - 1){
            li p2 = (b[i] + b[i + 1]) * li(b[i] + b[i + 1]);
            li s = b[i] * li(b[i + 1]);
            if (s * P2 > S * p2){
                A = b[i];
                B = b[i + 1];
                S = s;
                P2 = p2;
            }
        }
    
        printf("%d %d %d %d\n", A, A, B, B);
    }
}

1027D - Охота за мышью

Разбор

Решение (adedalic)

#include<bits/stdc++.h>

using namespace std;

#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
#define forn(i, n) fore(i, 0, n)

#define mp make_pair
#define pb push_back

#define sz(a) int((a).size())
#define all(a) (a).begin(), (a).end()
#define sqr(a) ((a) * (a))

#define x first
#define y second

typedef long long li;
typedef long double ld;
typedef pair<li, li> pt;

template<class A, class B> ostream& operator <<(ostream& out, const pair<A, B> &p) {
    return out << "(" << p.x << ", " << p.y << ")";
}
template<class A> ostream& operator <<(ostream& out, const vector<A> &v) {
    out << "[";
    forn(i, sz(v)) {
        if(i) out << ", ";
        out << v[i];
    }
    return out << "]";
}

const int INF = int(1e9);
const li INF64 = li(1e18);
const ld EPS = 1e-9;

int n;
vector<int> a, c;

inline bool read() {
    if(!(cin >> n))
        return false;
    c.assign(n, 0);
    a.assign(n, 0);

    forn(i, n)
        assert(scanf("%d", &c[i]) == 1);
    forn(i, n) {
        assert(scanf("%d", &a[i]) == 1);
        a[i]--;
    }
    return true;
}

vector< vector<int> > cycles;

vector<char> used;
vector<int> path;

void dfs(int v) {
    path.push_back(v);
    used[v] = 1;

    int to = a[v];
    if(used[to] != 2) {
        if(used[to] == 1) {
            cycles.emplace_back();

            int id = sz(path) - 1;
            while(path[id] != to)
                cycles.back().push_back(path[id--]);
            cycles.back().push_back(to);
        } else
            dfs(to);
    }
    path.pop_back();
    used[v] = 2;
}

inline void solve() {
    used.assign(n, 0);

    forn(i, n) {
        if (!used[i])
            dfs(i);
    }

    li ans = 0;
    for(auto &cur : cycles) {
        int mn = c[cur[0]];
        for(int v : cur)
            mn = min(mn, c[v]);
        ans += mn;
    }
    cout << ans << endl;
}

int main() {
#ifdef _DEBUG
    freopen("input.txt", "r", stdin);
    int tt = clock();
#endif
    cout << fixed << setprecision(15);

    if(read()) {
        solve();

#ifdef _DEBUG
        cerr << "TIME = " << clock() - tt << endl;
        tt = clock();
#endif
    }
    return 0;
}

1027E - Противоположная раскраска

Разбор

Решение (PikMike) O(n^3)

#include <bits/stdc++.h>

#define forn(i, n) for (int i = 0; i < int(n); i++)

using namespace std;

const int N = 500 + 7;
const int MOD = 998244353;

int n, k;
int dp[2][N][N];
int cnt[N];
int pr[N];

void add(int &a, int b){
    a += b;
    if (a >= MOD)
        a -= MOD;
}

int main() {
    scanf("%d%d", &n, &k);
    
    dp[0][0][0] = 1;
    forn(ii, n){
        int i = ii & 1;
        int ni = i ^ 1;
        memset(dp[ni], 0, sizeof(dp[ni]));
        forn(j, n + 1){
            forn(k, n + 1){
                add(dp[ni][j + 1][max(j + 1, k)], dp[i][j][k]);
                add(dp[ni][1][max(1, k)], dp[i][j][k]);
            }
        }
    }
    
    forn(i, n + 1)
        forn(j, n + 1)
            add(cnt[i], dp[n & 1][j][i]);
    
    forn(i, n + 1){
        add(pr[i + 1], pr[i]);
        add(pr[i + 1], cnt[i]);
    }
    
    int ans = 0;
    for (int i = 1; i <= n; ++i)
        add(ans, cnt[i] * (long long)(pr[min(n + 1, (k - 1) / i + 1)]) % MOD);
    
    ans = (ans * (long long)((MOD + 1) / 2)) % MOD;
    printf("%d\n", ans);
    
    return 0;
}

Решение (BledDest) O(n^2)

def norm(x):
    return (x % 998244353 + 998244353) % 998244353

n, k = map(int, input().split())

dp1 = [0]
dp2 = [0]

for i in range(n):
    l = [1]
    cur = 0
    for j in range(n + 1):
        cur += l[j]
        if(j > i):
            cur -= l[j - i - 1]
        cur = norm(cur)
        l.append(cur)
    dp1.append(l[n])
    dp2.append(norm(dp1[i + 1] - dp1[i]))

ans = 0
for i in range(n + 1):
    for j in range(n + 1):
        if(i * j < k):
            ans = norm(ans + dp2[i] * dp2[j])

ans = norm(ans * 2)

print(ans)

1027F - Сессия в БГУ

Разбор

Решение (Vovuh)

#include <bits/stdc++.h>

using namespace std;

#define forn(i, n) for (int i = 0; i < int(n); ++i)

const int N = 2 * 1000 * 1000 + 11;
const int INF = 1e9 + 1;

int n;
int a[N][2];
vector<int> s;
bool used[N];
bool exam[N];
vector<pair<int, int>> g[N];

bool deny(int v) {
    if (used[v]) return false;
    used[v] = true;
    for (auto it : g[v]) {
        int to = it.first;
        int ex = it.second;
        if (exam[ex]) continue;
        if (used[to])
            return false;
        exam[ex] = true;
        if (!deny(to))
            return false;
    }
    return true;
}

int cntv, cnte;

void dfs(int v) {
    ++cntv;
    used[v] = true;
    for (auto it : g[v]) {
        int to = it.first;
        int ex = it.second;
        if (exam[ex]) continue;
        exam[ex] = true;
        ++cnte;
        if (!used[to])
            dfs(to);
    }
}

bool check(int day) {
    memset(used, false, sizeof(used));
    memset(exam, false, sizeof(exam));
    forn(i, s.size()) if (i > day) {
        if (!deny(i)) {
            return false;
        }
    }
    
    forn(i, s.size()) {
        if (!used[i]) {
            cntv = 0;
            cnte = 0;
            dfs(i);
            if (cntv < cnte)
                return false;
        }
    }
    
    return true;
}

int main() {
    scanf("%d", &n);
    forn(i, n) forn(j, 2) {
        scanf("%d", &a[i][j]);
        s.push_back(a[i][j]);
    }
    
    sort(s.begin(), s.end());
    s.resize(unique(s.begin(), s.end()) - s.begin());
    
    forn(i, n) {
        forn(j, 2) {
            a[i][j] = lower_bound(s.begin(), s.end(), a[i][j]) - s.begin();
        }
        g[a[i][0]].push_back(make_pair(a[i][1], i));
        g[a[i][1]].push_back(make_pair(a[i][0], i));
    }
        
    int l = 0, r = int(s.size()) - 1;
    while (r - l > 1) {
        int mid = (l + r) >> 1;
        if (check(mid))
            r = mid;
        else
            l = mid;
    }
    for (int i = l; i <= r; ++i) {
        if (check(i)) {
            printf("%d\n", s[i]);
            return 0;
        }
    }
    puts("-1");
}

Решение (Vovuh) Алгоритм Куна

#include <bits/stdc++.h>

using namespace std;

mt19937 rnd(time(NULL));

const int N = 2 * 1000 * 1000 + 11;
const int INF = 1e9;

int n;
int a[N][2];

vector<int> nums;
int m;

vector<int> g[N];
int mt[N];
int used[N];
int T = 1;

bool try_kuhn(int v) {
    if (used[v] == T)
        return false;
    used[v] = T;
    
    for (auto to : g[v]) {
        if (mt[to] == -1) {
            mt[to] = v;
            return true;
        }
    }
    
    for (auto to : g[v]) {
        if (try_kuhn(mt[to])) {
            mt[to] = v;
            return true;
        }
    }
    
    return false;
}

int main() {
#ifdef _DEBUG
    freopen("input.txt", "r", stdin);
//  freopen("output.txt", "w", stdout);
#endif

    scanf("%d", &n);
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < 2; ++j) {
            scanf("%d", &a[i][j]);
            nums.push_back(a[i][j]);
        }
    }
    
    sort(nums.begin(), nums.end());
    nums.resize(unique(nums.begin(), nums.end()) - nums.begin());
    m = nums.size();
    
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < 2; ++j) {
            a[i][j] = lower_bound(nums.begin(), nums.end(), a[i][j]) - nums.begin();
        }
    }
    
    for (int i = 0; i < n; ++i) {
        g[a[i][0]].push_back(i);
        g[a[i][1]].push_back(i);
    }

    memset(mt, -1, sizeof(mt)); 
    int match = 0;
    for (int i = 0; i < m; ++i) {
        if (try_kuhn(i)) {
            ++T;
            ++match;
            if (match == n) {
                printf("%d\n", nums[i]);
                return 0;
            }
        }
    }
    
    puts("-1");
    
    return 0;
}

1027G - X-мышь в общежитии

Разбор

Решение (adedalic)

#include<bits/stdc++.h>

using namespace std;

#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
#define sz(a) int((a).size())

#define x first
#define y second

typedef long long li;
typedef long double ld;
typedef pair<li, li> pt;

const int INF = int(1e9);
const li INF64 = li(1e18);
const ld EPS = 1e-9;

li m, x;

inline bool read() {
    if(!(cin >> m >> x))
        return false;
    return true;
}

map< li, vector<pt> > dFact;
vector<pt> fact(li v) {
    if(dFact.count(v))
        return dFact[v];
    
    li oldv = v;
    vector<pt> fs;
    for(li d = 2; d * d <= v; d++) {
        int cnt = 0;
        while(v % d == 0)
            v /= d, cnt++;
        
        if(cnt > 0)
            fs.emplace_back(d, cnt);
    }
    if(v > 1)
        fs.emplace_back(v, 1), v = 1;
    return dFact[oldv] = fs;
}

vector<pt> merge(const vector<pt> &a, const vector<pt> &b) {
    vector<pt> ans;
    int u = 0, v = 0;
    while(u < sz(a) && v < sz(b)) {
        if(a[u].x < b[v].x)
            ans.push_back(a[u++]);
        else if(a[u].x > b[v].x)
            ans.push_back(b[v++]);
        else {
            ans.emplace_back(a[u].x, a[u].y + b[v].y);
            u++, v++;
        }
    }
    while(u < sz(a))
        ans.push_back(a[u++]);
    while(v < sz(b))
        ans.push_back(b[v++]);
    return ans;
}

li getPw(li a, li b) {
    li ans = 1;
    fore(i, 0, b)
        ans *= a;
    return ans;
}

li mul(li a, li b, li mod) {
    li m = li(ld(a) * b / mod);
    li rem = a * b - m * mod;
    while(rem < 0)
        rem += mod;
    while(rem >= mod)
        rem -= mod;
    return rem;
}

li binPow(li a, li k, li mod) {
    li ans = 1 % mod;
    while(k > 0) {
        if(k & 1)
            ans = mul(ans, a, mod);
        a = mul(a, a, mod);
        k >>= 1;
    }
    return ans;
}

li findOrder(li x, li mod, const vector<pt> &f) {
    li phi = 1;
    fore(i, 0, sz(f)) fore(k, 0, f[i].y)
        phi *= f[i].x;
        
    if(phi == 1 || x == 0)
        return 1;
    
    li ord = 1;
    fore(i, 0, sz(f)) {
        li basePw = phi;
        fore(k, 0, f[i].y)
            basePw /= f[i].x;
        
        li curV = binPow(x, basePw, mod);
        
        int curPw = -1;
        fore(k, 0, f[i].y + 1) {
            if(curV != 1)
                curPw = k;
            curV = binPow(curV, f[i].x, mod);
        }
        
        ord *= getPw(f[i].x, curPw + 1);
    }
    return ord;
}

vector<pt> fm;
vector<int> pw;

li calc(int pos, li dv) {
    if(pos >= sz(fm)) {
        vector<pt> cf = fm;
        fore(i, 0, sz(fm))
            cf[i].y = max(pw[i] - 1, 0);
        
        li phi = dv;
        fore(i, 0, sz(fm)) {
            if(pw[i] > 0) {
                cf = merge(cf, fact(fm[i].x - 1));
                phi -= phi / fm[i].x;
            }
        }
        li k = findOrder(x % dv, dv, cf);
        return phi / k;
    }
    
    li ans = 0;
    fore(i, 0, fm[pos].y + 1) {
        pw[pos] = i;
        ans += calc(pos + 1, dv);
        dv *= fm[pos].x;
    }
    return ans;
}

inline void solve() {
    fm = fact(m);
    
    pw.assign(sz(fm), 0);
    li ans = calc(0, 1);
    
    cout << ans << endl;
}

int main() {
#ifdef _DEBUG
    freopen("input.txt", "r", stdin);
    int tt = clock();
#endif
    cout << fixed << setprecision(15);
    
    if(read()) {
        solve();
        
#ifdef _DEBUG
        cerr << "TIME = " << clock() - tt << endl;
        tt = clock();
#endif
    }
    return 0;
}

Комментарии (50)

Показать архивные | Написать комментарий?

Roundgod

6 лет назад, # |

+67

You don't need a binary search in problem F. The complexity is O(nlogn) for coordinate compression. Build the graph, then apply DSU or SCC(Tarjan or Korasaju) with do the job. If there exists a connected component with number of edges greater than the number of vertices, then the answer is -1. If the number of edges is equal to the number of vertices, record the largest value, If the number of edges is equal to the number of vertices minus one, record the second largest value, the answer is the maximum over all connected components.

→ Ответить

rp789

6 лет назад, # ^ |

I was trying the same way but got tle in 45th test case. Any optimization you would suggest? I have used path compression and union by rank.

You were using map in your program, which adds an additional log factor together with large constant.

zeref_dragoneel

Can you please elaborate on the part of partial sums in problem E to solve the problem in N^2 time. I am unable to get it.

gohan123

← Rev. 2 →

+37

let lte[i] be the n.of binary strings of length n such that maximum segment of a single color has length <= i. (lte[i]-lte[i-1]) will be the n.of binary strings of length n such that maximum segment of a single color has length = i. Hence if we have lte array we can solve the problem. We can calculate lte[i] in O(n) as follows. let dp[j] be the n.of binary strings of length j such that maximum segment of a single color has length <= i.

If j>i dp[j]=dp[j-1]+dp[j-2]....dp[j-i]

else dp[j]=dp[j-1]+dp[j-2]..+dp[1]+1.

This is because in a string of length j at the beginning we can have at most i bits with the same color and after that, it's just dp[remaining length]. Now, lte[i]=dp[n]. Clearly, we can calculate the dp array by using partial sums in O(n). Since each element of the lte array takes O(n) time to calculate overall complexity is O(n^2). P.S: Don't forget to multiply by 2 at the end since all this is for a fixed color of the top left tile and it has 2 options (white or black).

AC: O(n^2)

Thanks a lot.

Can you just tell me why are we adding 1 in case of j <= i.

I think I got it. You are assuming that 1st element is fixed and 1 is for assuming all the j elements are same. Thanks.

+21

yes, glad that I was of some help :D

S.Jindal

Can you please explain the relation for j>i

dp[j] = dp[j-1]+...dp[j-i]

How ?

M3hran

This is because in a string of length j at the beginning we can have at most i bits with the same color and after that, it's just dp[remaining length].

I don't see why the reasoning is correct.

If you put X bit of same color in the beginning and fill the rest with dp[j — X] then it is possible to end up with a segment of same color that has length more than i. isn't it?

I guess you meant something else by beginning.

unreal.eugene

Не должны ли переходы в задаче E быть такими:

dp[i][j + 1][max(j + 1, k)] + = dp[i][j][k] и dp[i][1][max(1, k)] + = dp[i][j][k]?

awoo

Да, действительно, спасибо. Поправил, скоро обновится.

napatnicky

Can someone find out what is time complexity on my code? (problem C)

Here is my code 41811657 I think it should be O(T*n*log(n)) . But why it got TLE in case 6. Thank you!!

adedalic

Maybe because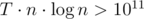 $\text{[math]}$ ?

In fact, for each test you create arrays a and cnt istead of making it global and clearing after each test.

g_abilash

Why is this getting tle sir??please help me 41788605

Kuroni

← Rev. 4 →

Try using ios_base::sync_with_stdio(false). I optimized my solution from TLE to AC.

TLE on test 6: 41767762

AC: 41767854

saluev

Wow, that helped me too. Thank you!

SJ151

Try scanf and printf rather than cin and cout it worked for me

but ,will i be able to use sort() function , if i am taking input through scanf() ,because i have coded in c++

Ya Of course

This code is not working , dude can you figure out the error

#include<bits/stdc++.h>
main()
{
   int i,arr[5];
   for( i=0;i<5;i++)
   {
      arr[i]=5-i;
   }
    sort(arr,arr+5);
   for(i=0;i<5;i++)
   {
      printf("%d  ",arr[i]);
   }
}

Add using namespace std;

VinBat

What does this line do in the code for Problem E? ans = (ans * (long long)((MOD + 1) / 2)) % MOD; Edit : Understood. For anyone having trouble it is modular inverse

bazsi700

+11

It divides ans by 2 modulo MOD, as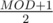 $\text{[math]}$ is the modular inverse of 2, because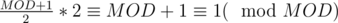 $\text{[math]}$

elizarov

← Rev. 3 →

+13

Kuhn's algo for F works only with this particular modification found in your solution -- you first check all the edges and if you find a suitable one, then you use it. Only if there are no suitable edges found, then you do a second loop and recurse into them (DFS). This versions passes tests. I don't know why.

However, a "vanilla Kuhn" that just uses a regular DFS (tries every edge to a non-visited vertex recursively) receives TLE, which is kind of expected, since it has complexity O(N*M) -- too big for this problem.

I've sent a solution for C (after the end of the contest) which sounds precisely like the given here (41817149), but it still didn't fit into given time :( What did I do wrong?

shazly555

In problem D, Why it is better to put trap on cycle, although there may be cheaper way to put trap on each path leads to this cycle like that. https://drive.google.com/open?id=19ff-GgeGhbhGXh5MykElhYXB3EErpq_9

Lukij

Because we don't know where the mouse starts (it may start in any vertex). Mouse can be on a cycle at the beginning and if the mouse is on a cycle at the beginning, it will be on this cycle forever. Thus it is necessary to put a trap on cycle, otherwise mouse beginning on cycle will never be caught. And according to your example, if we put a trap in vertex with cost 100, mouse will go through this vertex regardless of its beginning vertex, so it is enough to put there a trap.

Rajib_119

As far I know Complexity of Kuhn is O(n * n). How F is Solved with Kuhn? What's the trick or am I wrong? Thanks in advance.

I_love_myself

Kuhn works O(n*m). But tests for this assume prix is rough estimate. In real kuhn works very fast. There are also different heuristics.

tryhardtremor

Problem G: How to prove there is exactly u that u * x = v?

Help me. Thanks.

Because u = v·x^- 1

bitman_123

can someone help me in visualization of problem E dp.

arianetemadi

A little help on problem C! I don't know what I am doing wrong. I have a code in Python similar to the above solution, and I got TLE on test 5. Here is my code : http://mirror.codeforces.com/contest/1027/submission/41941233 Can someone find out?

BagishovMikail

I don't know why it gets TLE, but it also seems incorrect. Test:

1
7
1 1 999 999 7 7 7

Your output:

7 7 7 7

Trace:

1) c == 1, a[i] == 7 -> c := 7

2) c == 7, a[i] == 7 -> push

3) c == 7, a[i] == 7 -> push

But in fact you don't have 2 pairs

pieby2

In problem D, the editorial says that the mouse will stuck in a cycle. But my question is that, should the vertex in the cycle be reachable from all other nodes which are not part of the vertex's cycle because the girls are not aware of the position of the mouse? If it is required the how can we find it?

calier

It will always be stuck in a cycle, once it reached that cycle. So all you have to do is find all cycles, take the minimum number from each cycle and add to the answer :)

pk841

can someone please provide links to understand kuhn's algo?

Naman_123

Can anyone help me find the complexity of my code..?for Problem D...THis is my code in java.. http://mirror.codeforces.com/contest/1027/submission/42027693 Thanks

blackworm

sorry ignoring my algorithm (i mean whether is it correct or not) why i am getting TLE on test 2 ty 42082971

aboAdnan

Try to convert the input/output from cin/cout to scanf/printf and don't forget to extend the size of array ar to not get RTE.

Sorry i tryed to change them however i dont know why it is printing wrong answers! 42083838 amazing thing about it is that when i compiled it in my computer it printed right answers!!

You should use the identifier %lld with the type long long. And the size of the array is still not enough ;).

sorry still TLE 42085192

sorry i find the problem XD

XD the siiizzze

NGUYEN_THANH_LOI

Problem D:

Why does the mouse jump on a cycle at some point, no matter the starting vertex ?

rotavirus

Because it cant jump infinite times. In some number of jumps it will return to where it was

aryan29

https://mirror.codeforces.com/contest/1027/submission/41811657 can someone tell me why I am getting tle my method is almost same as that it tutotrial

TheScrasse

5 лет назад, # |

Why do I get WA on test 3 (problem E)? https://mirror.codeforces.com/contest/1027/submission/78959890
UPD: fixed, a -1 was missing (AC: https://mirror.codeforces.com/contest/1027/submission/78974251)

Блог пользователя awoo