Контест сегодня проводиться в не стандартное время : в 12:00 по МСК
Предлагаю после контеста обсуждать здесь задачи.
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Контест сегодня проводиться в не стандартное время : в 12:00 по МСК
Предлагаю после контеста обсуждать здесь задачи.
| Название |
|---|



Saratov SU #1: Agapov, Fefer, Chumachenko — True dream team
Ребята просто предложили написать вместе с ними. Для меня это, безусловно, позитивный опыт, поэтому глупо было бы не согласиться.
Блин, я люблю питерские туры. Респект за крутые задачи, которые, даже выступая в составе из одного человека, приятно и интересно решать!
А расскажите, кто как B делал? Я в ней написал некоторый вариант квадродерева (масштабируемся, пока не найдём квадрат с 60% единичек), долго пытался пихать с разными константами, а потом обнаружил тупейшую багу, поправил и сдал.
За "Орден Коварных Бобров" отдельное спасибо :-)
Зашло такое: Найдём самый заполненный квадрат 15х15 и будем его во все стороны поочередно расширять, пока в том, что мы добавляем 60% черного. Ну и на всякий пожарный после этого пытаемся его чуть чуть сжать, вдруг скор от этого улучшится
У нас примерно то же самое: только мы улучшаем по формуле, данной в условии. Сначала находим квадрат 15x15 с наибольшим счётом, а потом расширяем границы пока расширяется, причём так, чтобы значение формулы для расширенного квадрата было наибольшим...
Также, но выбираем для расширения стороны, в которой больше всего черного(отношения черного цвета ко всему). Перестаем расширяться, когда это отношение меньше 1/2 (или меньше или равно).
Так что тут почти любая жадина заходит
Мы для каждой клетки брали квадрат 15x15 с центром в ней и считали количество черных клеток в нем. Среди таких квадратов выбирали те, у которых черных > 2/3, строили bounding box для их центров. Потом отступали на небольшие dx, dy от границ и выбирали оптимальный вариант, считая по формуле.
У нас бинарная морфология зашла — возьмём структурным элементом квадрат 3х3, сделаем подряд эрозию, два наращивания и эрозию. Найдём прямоугольник описывающий оставшиеся точки. Если его в качестве ответа посылать было ВА 107, поварьировали на единички все координаты и нашли лучшый, зашло.
Хм. А что такое прямоугольник?
Видимо имеется ввиду bounding box.
Мы применили медианный фильтр, в итоге осталась почти одна связная область, которую оставалось аккуратно обработать)
А как нужно было решать задачу А про хеши? И означает ли это, что хеши на кодефорсе теперь совсем опасно использовать? :)
На GCJ была задача дано множество чисел надо найти 2 подмножества одинаковой суммы. Здесь делаем также будем искать 2 строки из 0 и 1. Выпишем хеш это получится просто сумма некоторых степеней p. Теперь решаем задачу также как на GCJ сдал ее eatmore.
Я сдал такое.
Давайте посмотрим на два полинома. Будем для простоты считать, что они оба имеют длину N = 105. Тогда их разность, которая должна оказаться нулём по модулю q, имеет вид
c0·pN - 1 + ... + cn - 2·p + cn - 1, где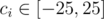 .
.
Будем искать небольшие суммы из какого-то количества степеней p, которые дают ноль в результате. Во-первых, давайте возьмём, посчитаем все степени p до (N - 1)-ой, отсортируем, и возьмём разности соседних. Так как степени p по модулю q ведут себя достаточно случайно, эти разности будут более-менее равные числа около . Это самое
. Это самое  имеет порядок
имеет порядок 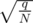 .
.
Отсортируем эти разности, возьмём снова разности соседних, получив тем самым какие-то выражения вида (pa - pb) - (pc - pd). Они будут ещё на несколько порядков меньше. И так далее. На k-ом шагу мы будем фактически оперировать суммами из 2k степеней p с коэффициентами ± 1.
Вот оказывается, что к третьему-четвёртому шагу гарантированно находится ноль среди таких разностей. А значит, что можно найти вот эти использованные 8 – 16 степеней p, и построить соответствующие строки, состоящие из множества букв a, перемежаемых чем-то другим в этих степенях.
Как-то так. I like it :-)
Я думаю, если выбирать основание и модуль случайные, то вполне безопасно.
Так прикол же в том, что здесь есть взломы и можно придумать тест, глянув в код.
Вроде как спасает большой модуль ~10^17.
UPD. Ок, всё понял. Случайные == рандомные.
Я сдал полнейший рандом. брал мапу, ключи — хеши, зачения — строки. генерил на каждой итерации рандомную строку рандомной длины, длиной не более 10 символом. смотрел, есть ли такой хеш в мапе. если есть — то профит!
Ты играл второй дивизион, с модулями порядка 1018 так не прокатит
У кого-нибудь были проблемы с тестом 5 в задаче H (Snakes)?
Нужно умножить координаты на 2. Иначе часть внешности, может быть недоступна скраю.
Что ты имеешь ввиду?
У нас было решение по H, которое получало WA 5. Его основная идея — dfs от краев. Его проблема была на тестах типа
3- не внутренность 1, но с краю нельзя добраться. Лечится умножением всех координат на 2(ну и хождением в dfs'e в том числе по нечетным)
Это все хорошо, конечно. Но у меня настолько кривые руки, что программа умудряется валиться по WA на 5-ом тесте, а Ваши тесты (включая нижеприведенный) проходит. Если что, вот код (не стреляйте, пишу как умею): http://pastebin.com/4zUaz5jh
Зачем там дфс? Мы отлично сдали вариант запоминая 1 координату каждой змейки, потом пускаем из нее линию например вверх до конца карты, если встречаем другую змейку -в стек ее, если на стеке 2 одинаковых -убираем, в итоге получаем в чем лежит каждая, теперь каждому проставляем кто внутри (очищаем стеки до размера 1, этому одному ставим в дети текущего, если до этого ребенок был — ставим -1). Далее печатаем если у змеи нет родителей или у родителя много сыновей (-1 в поле дети), прошло сразу, хотя были проблемы с лишними пробелами в выводе.
Ну мы ещё масштабировали картинку чтобы небыло случаев дурацких.
Например?
Видимо, речь идёт о случае, когда мы упираемся в отрезок какой-либо змеи, который сонаправлен с движением линии из точки.
У нас было ВА 5, когда не проходило такой тест: http://pastebin.com/GTurg3vZ
И расскажите G, пожалуйста.
Построили ДНФ. Выразили через штрих отрицание,и, или
Вариант 1. Выразили так, что A, B входят 2 раза в A^B,AvB . Тут чтобы посчитать A_1 v A_2 v ... v A_N нужно не по очереди, а деля на 2 равные половины
Пример выражения
Вариант 2. Выразили сперва истину и ложь, через них то же ^, v, теперь уже A, B входят по 1 разу и все получается линейно
А еще можно выразить отрикание, как стрелку от числа и 1. 1 делается как угодно. Всем привет от Copymaster.
Получается вот такое решение, которое укладывается в 600 символов (а не в 500000, как предлагалось).