The proof to the greedy approach in Problem C is interesting!

Excellently organized contest with short and precise problem statements.

Well done Ashishgup and Mahir83 !

Problem E. We can delete all loops because if we stay on vertex we can take all loops.O(n) solution we know that number of vertexes which has odd degree can be only 0, 2, 4. Because if 3 vertex has odd degree sum of all degree not divide on 2. It means if number of vertexes which has odd degree 0 or 2 graph has Euler path, it means we can take all edges. If number of vertex which has odd degree 4 we have two case. 1 case number of components equal 1 and number of components equal 2. If number of components 2. Each component has Euler path we take max. If number of components equal 1, we can take all edges except 1 edge. Sorry for my english.

F can be solved in O(n³), by counting strings based on the KMP state after reading whole string. As string is cyclic we want the KMP state to start and end with same state and somewhere in between the KMP state should be |S|. See my code for details

In Problem D, Why in the solution code of the author he say that when all of numbers are positive or all of them are negative then answer is ans-2*minValue ?????

I think The easiest way to solve problem B was to take 'n' in one set and the rest 1 to n-1 in another set. why does this work? As the sum of 1 to n-1 is n * (n-1)/2, so, the gcd of n and n*(n-1)/2 is always greater than 1. My Submission : http://mirror.codeforces.com/contest/1038/submission/42567986

I m not able to get AC even after referring to solution for problem C. Please help !!!

I have attached link to my solution 42593499

still, haven't understood the problem D... So, anybody can give the proof of correctness for D???? thanks in advance....

Thanks for allowing exponential solutions to pass for F! http://mirror.codeforces.com/contest/1038/submission/42588924

Let m=s.size().

If m>=20, we just fix s as the prefix of t and brute force the remaining 2^(n-m) possibilities and carefully count the number of rotations that will work. This part is O(2^(n/2)*n)

Else, we brute force the prefix of length (m-1) of t and there are 2^(m-1) possibilities. This is a standard trick to convert cyclic dp to array dp, which is easier to think of for stupid people like me.

Alternative solution for E (harder to implement but was easier to come up with for me): While there are 3 or more edges between two colors, we can remove two most valuable edges and note that if any of these vertices is visited than we need to add the value of all corresponding removed edges. Now there are no more than 2 (edges per color-pair) * 6 (color-pairs) = 12 edges. The graph became small enough to bruteforce all possible edge-paths: After making 11 steps there will be only 1 edge left so we won't have a choice at that point. First 11 times there will be no more than 3 (number of other colors) edges to choose from. This gives an upper bound of 3^11 = 177147 node traversals. We will need to try starting at all four colors so the final number is 4 * 3^11 = 708588. In practise it works surprisingly fast: 31ms. If you for some reason would like to look at my solution: https://mirror.codeforces.com/contest/1038/submission/42595983

My alternative bruteforce Solution for E, without any nasty graph theory and bitmasks https://mirror.codeforces.com/contest/1038/submission/42586454

the Idea here of this solution is that we can divide the blocks into 6 type of block (block with color (1,2), (1,3), (1,4), (2,3), (2,4) (3,4) ) (since (1,2) is equal to (2,1))

for blocks that has the same color (1,1) (2,2) (3,3) (4,4). we could count it greedily since if we could choose one blocks of a type, we could choose all blocks of that type. Lastly we could brute force all of the possible quantity for block with type (1,2), (1,3) (1,4), (2,3), (2,4), (3,4) and check whether it possible to create a valid sequence of blocks. then, for each case find the maximum.

At the worst case, the blocks will be divided equally (16-17 blocks for each type) The overall time complexity is O(6 * (n/6)^6) ~= 128600823.04526755, which is fit the time limit

Correct me if i wrong and sorry for my bad england.

Can Anyone help me with the dp approach that author was tring to convey( about the 4*n states)..It shall be really helpful!

In problem D, Can anyone prove how "any combination of + and − is obtainable"?

And what train of thought leads to this conclusion?

In problem D I'm getting WA in test case 35.It's very big test case.So,Can anyone give small counter test case?

My submission

Can anyone give a proof of why the greedy solution is correct for Problem C. I read the editorial and comments but I'm still confused why it works. Thanks in advance!!

Please put this blog into Contest materials.

F can also be solved in O(n²) using inclusion-exclusion principle. Implementation: https://mirror.codeforces.com/contest/1038/submission/42615092

Explanation:

Let n be the length of target string and m the length of pattern. Let A_i be a set of cyclical strings containing pattern at position i. The answer to the problem is the size of . We can write it using inclusion-exclusion principle as:

Now consider dynamic programming f(k) as contribution (in the sum above) of subsets J of {0, ..., k} containing 0 and k, but forgetting about bits on positions  > k (so f(k) is contribution divided by 2^{irrelevant bits}). Having values of f(k) computed we can get the answer in the following way:

(for each k we need to multiply f(k) by count of "non-wrapping shifts" of positions set (all of them contain 0 and k) and fill in the forgotten bits). How to compute f(k)? Let valid(i) be the set of positions j such that we can place pattern at position i and j simultaneously.

f(k) is non-zero only for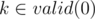 since counted sets always contain 0 and k. For such k we consider all possible previous positions of pattern and fill not covered bits. Whole sum is negated since we increase power of -1 in inclusion-exclusion equation. Notice that valid(i) is just cyclical shift of positions in valid(0), it's introduced for notation. valid(0) can be computed naively in O(nm) or O(n + m) using KMP.

Can someone tell me how this work to solve the problem E?

In problem C: what's the induction proof to show DP == Greedy ?? Some hints plz

Can someone explain this solution to problem F? 42584804

UPD. I wrote something stupid and found editorial could do nearly the same thing.

Whatever, for problem C, follow the proving idea in editorial, we can have a shorter solution. my submission (This code is different from the proof in editorial, but I think they are similar if you wrote a version based on proving idea in editorial.)

How does bool checker() in author's solution on problem E work ?

just wondering if there exists a solution for problem E that involves minimum cost flows, thanks and good round btw :)

Details for pF please

There is an interesting O(2^n / 2n²) solution for the Problem F. In the case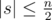 , enumerate the rest part and count different number of string; In the case 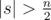, enumerate the first L-1 chars of the string and do a O(n²) dp. The total time complexity is O(2^n / 2n²) and I got AC. My code : http://mirror.codeforces.com/contest/1038/submission/42792131

" The key observation to solving the problem is that any combination of + and − is obtainable, except where all signs are + or all are − " How to prove this ?

Another solution for the Problem E. Just brute force and greedy.

For every node (1 2 3 4) , we fix its matching priority. For example, node 1, match 2 first, then match 4, and then 3.

Why? If we choose three edges in our answer, for example, 1-2 , 1-3 , 1-2 . This means we can at least go back to node 1 twice. So why not choose the matching nodes in a fixed order ? (1-3, 1-2, 1-2) This means we must select node 3 before select node 2 when we are at node 1. This can be done for every nodes. And brute force matching priority only cost O((3!)^4) , the specific complexity depends on your implementation.

check my code for more details. 42952879

Sorry for my extremely poor English.

1038B O(1) solution (it`s not about output data), but for n>2 answer is Yes, and you need to put (n+1)/2 to first set, and all other numbers to second set, and No otherwise

For D problem The Slimes one for the test case 4

1 1 -1 -1,According to editorial the answer should be 4 but there is no sequence in which the slimes can eat to get the answer 4 or maybe I am missing something,According to me the answer for this test case should be 2

I didn't understand the dp solution for problem D.

My solution for problem C(Gambling)

https://pastebin.com/Z3FLxML1

My solution to problem C(Gambling) My Code

So,for problem D I have the proving process, and the Solution ignore it,the code ID:66302024 Welcome to Hack~

`Most easy approach vll =vector

int main() { FAST; ll n; cin>>n; vll a(n); for(ll i=0;i<n;i++) cin>>a[i]; sort(a.rbegin(),a.rend()); vll vis(n,0); for(ll i=1;i<n-1;i++) { if(a[i]>0) { a[n-1]-=a[i]; vis[i]=1; } }

for(ll i=1;i<n;i++)
{
    if(vis[i]==0)
    a[0]-=a[i];
}
cout<<a[0];
return 0;
}

Problem $$$E$$$ was quite nice!

I have a different solution than the editorial. In fact, it's better than the editorial and runs in $$$\mathcal{O}(N)$$$.

As the editorial suggests, this problem effectively reduces to finding the longest (i.e. highest weighted) path which does not repeat edges amongst a graph with only $$$4$$$ nodes and at most $$$100$$$ edges. Instead of trying to construct this path, we can try to construct some subset of edges which can form a path. So in a sense we reverse engineer the problem.

In order for the edges to form a path, we must have at most $$$2$$$ nodes with odd degree. In fact, we can't have an odd number of nodes of odd degree either for obvious reasons, so we basically have either $$$0$$$ or $$$2$$$ nodes with odd degree.

Additionally, and perhaps obviously, the edges, once connected, cannot have two nontrivial connected components. Basically, we cannot have the edge $$$[1, 2]$$$ and $$$[3,4]$$$, since we have no way of traveling between those edges.

With these observations, we have vastly reduced the number of requisite states. In fact, our state only needs to contain information about the mask of edges visited, the parity of the degrees of the nodes, and which prefix of nodes we've visited.

I will leave as exercise to reader how to transition between those states. It's quite straightforward if you understood the preceding part.

Code: 164193566

D: "The key observation to solving the problem is that any combination of + and − is obtainable, except where all signs are + or all are − (exception n=1, where the answer is the value of the slime itself)"

Give proof.