katana_handler's blog

Sieve Of Eratosthenes ( O(n) vs O(n log log n) )

By katana_handler, history, 6 years ago, In English

Hello Everyone!

I recently found an algorithm for finding the primes in O(n) in GeeksforGeeks and it was convincing also and then there is always the Sieve of Eratosthenes running in O(n log log n). The O(n) sieve is however a modification of the normal Sieve of Eratosthenes. But now what happened was that when I implemented the O(n) Sieve it should have run faster than the normal one(at least by a small margin) but it was always slower than the normal Sieve! Can someone please tell me why is it so?

But there a small catch also when we run both the programs for N up to 10^8 the normal sieve is faster by around 0.5 — 0.7 seconds but where as when we give N=10^9 though both takes more memory and time but the O(n) sieve works 0.5 3.0-5.0 seconds faster! so the second question that comes it that, Is the O(n) sieve better for larger numbers only??

PS: The codes I used is the same as shown in the GeeksforGeeks site!

EDIT: we just implemented it on our own and the result for N<=10^8 is the same but the for 10^9 O(n) runs in 12 sec and the normal one runs in 16 sec!!

  • Vote: I like it
  • +17
  • Vote: I do not like it

Comments Comments (6)
| Write comment?
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Why is this ?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Each number will be marked only one time:

    • For prime numbers it is obvious;
    • Let's X = p1·p2·...·pk and p1 ≤ p2 ≤ ... pk.
      It will be marked exactly one time, when j = p1 and i = p2·p3·...·pk.
      It is correct because j ≤ lowestPrime[i], so X = j·i could be marked only at that time.
    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      yeah exactly! but still this runs slower than the normal one for smaller numbers!! any explanation for that!?

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +11 Vote: I do not like it

        Because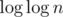 is very small factor, and constant factor is very important. Even for big numbers clever 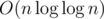implementation (such as segmented sieve) will be much faster than O(n).

        → Reply
»
6 years ago, # |
  Vote: I like it +3 Vote: I do not like it

The implementation in GeeksforGeeks is weird. There's no need to use long longs at all.

Replacing all long longs by ints, and the condition i*prime[j] < N by

const int max_pj = N / i;
for (int j=0;
    j < np && prime[j] <= max_pj && prime[j] <= SPF[i];
    j++)

makes the program run in half the time for N = 5e8.

→ Reply
»
6 years ago, # |
← Rev. 3   Vote: I like it +29 Vote: I do not like it

Like it has been described in other comments, complexity says nothing about hidden constant and things like that. You shouldn't expect solution with better complexity to work faster no matter what input data and constraints are. You may sometimes see problem setters having hard times while trying to make their nice-shiny-and-beautiful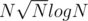 actually work faster than trivial N2.

In case you want to make a decision about which of two algos to use when the best performance is needed, your strategy should look like this: get the best possible implementation of either of two algorithms, compare them and see which one is better in one case or another. Simply taking random code from the Internet is not always the best idea; taking this code from site like GeeksforGeeks is just a bad idea.

In most of the cases it simply doesn't matter, as constraints are picked in such a way that any reasonable implementation will get the work done, unless it is a problem specifically about implementing some sieve in a fast way.

Both of the codes that you provided are far from being optimized for better performance, and it is quite possible that when writing them their authors simply didn't care about it (as they were doing it just for educational purpose). Comparing them to figure out which algorithm is "better" doesn't make much sense.

→ Reply