muratt's blog

Couple of Problems That We Couldn't Solve
By muratt, 6 years ago, In English

Me and my friends were working for upcoming ICPC regional. We got stuck at these two problems.

1-(This one is solved in comment sectiom) You are given an array with n elements, you can increase one element's value by one with one cost. Your goal is to make xor of all elements 0 with minimum cost. n <= 1000, ai <= 109

Here is the link for the problem: http://algotester.com/en/ArchiveProblem/Display/40442

2-You will be given n intervals like [li, ri]. You have to divide these intervals into two subsets A and B such that every interval belongs to exactly one subset and the intersection of A and B maximized and print this subset. The intersection of two sets of intervals is sum of every pair of intervals' (one from A, one from B) intersection length. n <= 100000, 0 <= li <= ri <= 109

Link to this problem: http://algotester.com/en/ArchiveProblem/Display/40384

Thank you for your help (:

  • Vote: I like it
  • +46
  • Vote: I do not like it

»
6 years ago, # |
  Vote: I like it +21 Vote: I do not like it

The first one is an awesome problem as you need many observations in order to solve it. I am going to describe the solution very briefly.

Let us fix an optimal solution (that is a choice of b[i] ≥ a[i] such that their xor is 0 and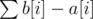 is minimized). Then we make the following observations:

  1. We can assume that if a[i] ≤ a[j] then b[i] ≤ b[j].
  2. For any i let us define x[i] as the largest bit in a[i]^b[i] (define it as  - 1 if a[i] = b[i]). Each positive value of x[i], apart from the largest one, is assumed at most one time. The largest one can be assumed at most twice.
  3. For any i it holds x[i] ≤ 31.

With this observations (that I leave to prove to the reader) it is easy to create a solution. Indeed, once we have fixed the largest value of x[i], the previous observations are enough to uniquely define an optimal strategy (fixing greedily all bits from the largest to the smallest).

In some sense the described algo is almost greedy, indeed, after a single choice, a greedy algorithm works.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    "Each positive value of x[i], apart from the largest one, is assumed at most one time. The largest one can be assumed at most twice."

    What do you mean here by saying "assumed"?

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      "V is assumed at most one time" = "there exists at most one i such that x[i] = V".

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        oh now i think i got it, thank you!

        → Reply
»
6 years ago, # |
  Vote: I like it +10 Vote: I do not like it

I think the second problem is this problem: http://mirror.codeforces.com/contest/429/problem/E. I have a comment about it here: http://mirror.codeforces.com/blog/entry/12265?#comment-169310

→ Reply