Блог пользователя Siriuslight

Problem BBRICKS from Codechef Long challenge
Автор Siriuslight, история, 6 лет назад, По-английски

How to solve this problem using matrix exponentiation. The recurrence relation is :

f(n, k, 0) = 2 * f(n - 1, k, 1) + f(n - 1, k, 0)

f(n, k, 1) = f(n - 1, k, 1) + f(n - 1, k, 0)

1 < n < 1e9

1 < k < 1e3

  • Проголосовать: нравится
  • 0
  • Проголосовать: не нравится

»
6 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

Matrix exponentiation is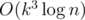 and it can be optimized to 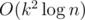, but it's too slow and may still get TLE.

I used a O(k) solution.

→ Ответить
»
6 лет назад, # |
← Rev. 2   Проголосовать: нравится +1 Проголосовать: не нравится

I solved it by Lagrange Interpolation

Let f(n, k) denote the answer then we have the recurrence

f(n, k) - f(n - 1, k) = f(n - 1, k - 1) + f(n - 1, k - 2)

Now $f(n, 1) = 2n $ , which is linear, which implies that f(n, 2) must be quadratic, which implies that f(n, 3) must be cubic and so on..

So for fixed k, f(n, k) will be a kth degree polynomial in n, and therefore i precomputed f(n, k) for n, k upto 2000 and then I answered each test case in O(n) using Lagrange Interpolation.

So overall time complexity O(K2 + TN)

My solution for reference

→ Ответить
  • »
    »
    6 лет назад, # ^ |
    ← Rev. 2   Проголосовать: нравится 0 Проголосовать: не нравится

    I have heard of this term first time. Maths is really very important for progress in CP. BTW thank you for your solution.

    → Ответить
»
6 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

It can be done by combinatorics

https://www.codechef.com/viewsolution/20517309

→ Ответить