Though some articles of this topic are already available, as a beginner I found them quite hard. So I decided to write down my thoughts here, in case someone finds it useful. Sorry for poor formatting and poor English.

Using one BIT we can do range increment and point query: For increasing a[l...r] by val, tmp[l] += val, tmp[r+1] += -val. After any number of range updates, prefixSum(i) of tmp[] denotes total increment in a[i] till now. BIT supports both point increment and prefixSum query.

Using another BIT with this BIT, we can also calculate range query. Let, prefixSum(i) from first BIT is a[i] = a[i]*(i-(i-1)). Our target is to calculate prefixSumOFa(i) in O(logn).

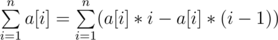
Let, addend[i] = a[i - 1] * (i - 1) - a[i] * (i - 1). so, 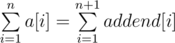, assuming 1-based indexing and a[0] = a[n+1] = 0

if (a[i]==a[i-1]), addend[i] == 0. So, writing all non-zero elements of addend[] for an example a[]:

i                |   1   |   2   |   3   |   4   |   5   |   6   |   7   |   8   |   9   |

a[i]             |   0   |   3   |   3   |   0   |   0   |   2   |   2   |   2   |   0   |
addend[i]        |       | -3*1  |       |  3*3  |       | -2*5  |       |       |  2*8  |

Observation: prefixSumOFa(i) = a[i]*i + prefixSumOFaddend(i). In case you are confused about where a[i]*i come from, notice that if a[i] would be last element of a[], a[i]*i would be written in addend[i+1].

Now, to calculate prefixSumOFa(i), we can get a[i] from first BIT, for getting prefixSumOFaddend(i), we need to keep another BIT, BIT2. For increasing [l...r] by val, we need to update BIT2(l) += (-val*(l-1)) and BIT2(r+1) += val*r.

This method works even if updates overlap, as when updating [l...r], for i = [l+1...r], (a[i-1]-a[i]) remains the same, so append[i] = (a[i-1]-a[i])*(i-1) remains same. Just like previous example, only updating BIT2(l) and BIT2(r+1) is necessary. For example if we increase range [5...7] by 5 in previous example of a[]:

a[]              |   0   |   3   |   3   |   0   |   5   |   7   |   7   |   2   |   0   |
addend[]         |       | -3*1  |       |  3*3  | -5*4  | -2*5  |       |  5*7  |  2*8  |