teja349's blog

Invitation to CodeChef October Lunchtime 2018!
By teja349, history, 6 years ago, In English

Hello Codeforces Community!

We would like to invite you to our next monthly contest and we’re sure you’ll enjoy — the October Lunchtime 2018 sponsored by Sharechat! Along with interesting problem sets, we have exciting full-time job opportunities by ShareChat for professionals across the globe. More details can be found on the October Lunchtime contest page.

Joining me this time on the problem setting panel are:

  • Problem Setter: kingofnumbers (Hasan Jaddouh), PraveenDhinwa (Praveen Dhinwa)

  • Problem Tester: teja349 (Teja Vardhan Reddy)

  • Editorialist: taran_1407 (Taranpreet Singh)

  • Statement Verifier: Xellos (Jakub Safin)

  • Russian Translator: Mediocrity (Fedor Korobeinikov)

  • Mandarin Translator: huzecong (Hu Zecong)

  • Hindi Translator: Akash Shrivastav

  • Bengali Translator: Imran Hasan

  • Vietnamese Translator: VNOI Team

Contest Details:

Time: 27th October 2018 (1930 hrs — 2230 hrs). (Indian Standard Time — +5:30 GMT) — Check your timezone.

Contest link: https://www.codechef.com/LTIME65

Registration: You just need to have a CodeChef handle to participate. For all those, who are interested and do not have a CodeChef handle, are requested to register in order to participate.

Prizes: * Top 10 performers in Global and Indian category will get CodeChef laddus, with which the winners can claim cool CodeChef goodies. Know more here: https://discuss.codechef.com/questions/51999/how-do-i-win-a-codechef-goodie. (For those who have not yet received their previous winning, please send an email to winners@codechef.com)

Good Luck! Hope to see you at the contest!

  • Vote: I like it
  • +22
  • Vote: I do not like it

»
6 years ago, # |
  Vote: I like it +29 Vote: I do not like it

ACMIND18 part 2?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    We'll see

    → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +60 Vote: I do not like it

    I want to be a Um_nik but I stop myself here. Hope one day I will give my opinions like him.

    → Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it +155 Vote: I do not like it

    The real question though is that if you have never solved the third problem in any contest ever, does there exist a contest not like ACMIND18 for you?

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +28 Vote: I do not like it

      There is no need to be Um_nik teja349. The comment by jtnydv25 hits it home.

      I have seen many times that Jatin goes after the toughest question in every Div1 contest. No matter how tough the question is. This really shows the mentality these red coders have. They seek challenges and solve them. Normal people think of a problem as some kind of a curse. And they just want to get over with it.

      → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Ratings for Encoder are not updated.Will it happen before the contest?

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it +5 Vote: I do not like it

How to solve third problem(div. 1)?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    A bit hard to explain!! Here's what I did

    1. Count all -1's (let it be CT) and subtract the non -1 elements from S.

    2. Then generate all distinct sets (multisets) of size CT having sum S. The number of such sets is small under the given constraints (order 10^3) and all such sets can be generated using simple backtracking.

    3. For each such set count the number of ways you can rearrange the elements... Simple combinatorics!! (Maintain count of each element in the set)

    4. To each set append the non -1 values and find the ans (lets call it Temp_ans) for each set(brute force).

    5. Final ans=Summation( (ways*Temp_ans)%MOD).

    Link to my solution: https://www.codechef.com/viewsolution/21244428

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      is this the expected solution ??

      → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      A simple doubt: how you estimated no. of distinct sets will be order of 10^3 ? or Is there any formula to calculate no. of distinct solutions ( By distinct it means if eq'n- x+y+z = 8 then 1,2,5 and 2,1,5 and 5,1,2 should be treated same and counted as one)

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +3 Vote: I do not like it

        I don't think there exists an explicit formula, but wolfram alpha can calculate it. The order may be higher than 10^3, but then N will be small. For example for N = 10, S = 50 and Ai =  - 1 there are  17000 partitions, but the complexity of the solution is O(XN2) where X is the number of partitions. So basically if X is big, then N must be relatively small, and vica versa, so all in all it will pass.

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Thanks

          → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          "So basically if X is big, then N must be relatively small, and vica versa"
          Can you tell me why? How are number of partitions and N related?

          → Reply
          • »
            »
            »
            »
            »
            »
            6 years ago, # ^ |
            ← Rev. 2   Vote: I like it 0 Vote: I do not like it

            The number of partitions will be big if S is relatively big and the number of parts is relatively small. The second means that there are few -1 s, and the first means that there must be few non -1s because every number is positive.

            → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I have a polynomial solution.

    Let's look at the following solution to find the niceness of a given array (no  - 1s) .. loop for the gcd g and then count the number of pairs of elements with gcd = g (let it be ans[g]) .. add g * ans[g] to the answer. However, finding the number of pairs of elements with gcd = g sounds tough .. the idea is to find the number of pairs of elements such that g divides both (much easier problem) and then subtract ans[2 * g], ans[3 * g], ... from it. Which means that we find all pairs with gcd multiple of g and then subtract those with gcd! = g to end up with those with gcd = g. How to adjust this to our problem ? Instead of counting the number of pairs with gcd multiple of g in the given array, we want to find the number of pairs with gcd multiple of g in all possible arrays .. the rest of the solution is the same. Notice that it's sufficient to know the count of multiples of g for this. If all the elements are  - 1, we can calculate dp[g][n][c][s], the number of arrays with n elements, c of which are multiples of g, and their sum is s. The transitions are simple: just bruteforce every next element and change the state based on it. We'll add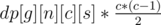 to our count for all c ≤ n, but what about the elements that aren't  - 1? well, they only change the starting n, s, and c (we'll reduce their count from n, their sum from s, and the count of multiples of g in them from c). The complexity is upper-bounded to O(n2s3 + t(sn + slog(s))) but, of course, it's faster. code

    → Reply
»
6 years ago, # |
  Vote: I like it +45 Vote: I do not like it

Bonus for third problem:
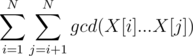
Instead of given formula try to solve problem for range formula(instead of pairs), like this:



During the contest I spent my lot of time to this problem. I debugged my code for 1 hour and I could not found any mistakes. My code giving 21 for second test. After 1 hour I realized that problem asking for pairs not ranges :)

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    I didn't read tasks for Lunchtime, but this task can be solved with binary search + segment tree in O(nlog2(n)·logXi):

    For each position i, it will be at most logXi postions j with different value gcd(Xi, ..., Xj). and values will go decreasing. After it, just do binary search + segment tree to find all positions j. Probably it can be done without binary search without one logn.

    Do you have something better?

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 5   Vote: I like it +11 Vote: I do not like it

      Try to read problem, because N ≤ 50 and A[i] ≤ 50 :)

      → Reply