Given n integer positive numbers ,find the minimum numbers of operations such that no two numbers have their product making a perfect square. In 1 operation you can pick any number and add or subtract one from it. All the numbers must be positive after all the operations are performed. 1<n<=100 and value of numbers are in range of 1 to 100000. Any help/discussion will be appreciated!!
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
36:52:57
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
36:52:57
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 04:42:03 (j3).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Here's what I got, not a full solution but I feel it's close enough.
First notice that the property for two numbers' product to give a square is transitive. In other words:
Given that ab = x2 and bc = y2 it is clear that ac = z2 for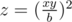
In such case we can create groups of numbers such that any two numbers in a group will form a square. For example such groups are {1, 4, 9, 16...} or {2, 8, 18...}. Our goal is to move the numbers we have around so that there are no two numbers in the same group.
Now the most straight-forward solution you can make is to just transform the problem to minimum cost maximum matching. The problem is that actually those groups are quite small in size and large in amount. Running a short code gives that among the numbers 1 to 100000 there are actually about 60000 different groups. This means that creating a full graph (edge from each number to each group with minimum cost to move the number to that group) is too expensive.
It is, however, intuitively clear that a number will not move too much. With so many groups, moving each number only a little will be usually optimal. I believe it shouldn't be too hard to come up with a strategy that only uses plausible edges/vertices in this bipartite graph so that the matching algorithm will run sufficiently fast.
It could be that the author solution takes a different approach after the first observations, but I think this one can be made to work as well. If you give me an online judge where I can submit, I might be able to test further.
The same question was posted about two weeks ago.
It was given before here.
Min-cost flow solution here. Basically we will use the idea described by Enchom in the comments above, but we will create a slightly different graph.
There are two layers (but the graph isn't bipartite).
The first layer represents all numbers from 1 to 100000 and there is an edge with capacity equal to ∞ and cost equal to 1 between the vertex for x and the vertices for x + 1 and x - 1.
The source is connected to the the vertices from the first layer that appear in the input with an edge with capacity 1 and cost equal to 0. We should note that there are only N such edges. This is important for the complexity.
The second layer represents the "reduced integers" — they are basically the products of the divisors that appear odd number of times. Now we will have edges from first layer to second layer such that vertex for number x from the first layer is connected to its reduced value with cost equal to 0 and capacity equal to 1.
Finally we add edges from the second layer to the sink with capacity 1 and cost 0.
The answer is the minimum cost of any maximum flow from the source to the sink.
The complexity will be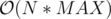 or
or 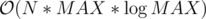 depending on the shortest path algorithm we use in the min-cost flow algorithm (Dijkstra or SPFA). This is true, because the maximum flow will be N so we will have at most N runs of our algorithm.
depending on the shortest path algorithm we use in the min-cost flow algorithm (Dijkstra or SPFA). This is true, because the maximum flow will be N so we will have at most N runs of our algorithm.