Dalgerok's blog

Round #532: coincidences?
By Dalgerok, history, 6 years ago, In English

After round I saw some interesting links in the comments.

Problem C: https://www.quora.com/What-is-the-radius-of-the-circle-surrounding-a-circle-if-all-the-surrounding-circles-are-equal

Problem F: After understanding that you must find "subset with maximum XOR" on range from L to R, this subtask is becoming very easy to google it (e.g https://www.geeksforgeeks.org/find-maximum-subset-xor-given-set/)

Actually the SAME problem: https://blog.csdn.net/ShadyPi/article/details/79939990

You can see many accepted submissions with this idea :|

Problem E: https://www.geeksforgeeks.org/assign-directions-to-edges-so-that-the-directed-graph-remains-acyclic/ the same idea to direct edges in order to topological sorting.

Thanks to Rinne and M_H_H_7 for the links in the comments (https://mirror.codeforces.com/blog/entry/64495?#comment-484476, https://mirror.codeforces.com/blog/entry/64495?#comment-484418).

  • Vote: I like it
  • +55
  • Vote: I do not like it

Comments Comments (7)
| Write comment?
»
6 years ago, # |
  Vote: I like it +37 Vote: I do not like it

A bit notorious.

→ Reply
»
6 years ago, # |
  Vote: I like it -26 Vote: I do not like it

It would be useful to enclose the spoilers in spoiler tags.

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it -26 Vote: I do not like it

We have discussed the problem D with similar constraints (actually, they doesn't matter) in our math training session. Also, the solution was exactly the same as the tutorial.

I found the link while writing this comment, check 091 here: http://olympiads.win.tue.nl/imo/soviet/RusMath.html

→ Reply
»
6 years ago, # |
  Vote: I like it +92 Vote: I do not like it

Maybe it is only my problem, but why are you trying so hard to google the problems? Both C and E are faster to solve by yourself than find the solution on the internet.

About F: article from geeksforgeeks doesn't tell you how to solve the problem (maybe its because geeksforgeeks is trash? idk). There are some words about Gaussian elimination but I don't think that you can understand that unless you already know that XOR is sum of vectors in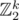 . And about the same problem — it is in Chinese! Do you think that problemsetters must learn Chinese? Even the guy who wrote the original comment about that problem existence mentioned that it is 100% coincidence.

About D from comments: the problems are not the same. This is how problemsetting works: you take something already existing and change it to get new problem.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +37 Vote: I do not like it

    Problems are same, actually. The ASU problem is solved by finding the algorithm.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      Rooks are moving by chess rules instead of jumping to any point. This one is enough for problems to be different. Algorithms maybe the same, but the proofs that it works are different.

      → Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    I didn't google this problems. Links were in the comments.

    The fact remains. Person who is not able to solve this problems can simply google them.

    → Reply