Consider a directed tree say for example P1--> P2--> P3--> P4--> ... --> Pn (consider this chain for simplicity), initially, it is like this, directed and atmost one edge going out of every node(for some nodes there might be no outgoing edges). Here it is like if the information starts at P1 it flows till Pn, similarly, if information starts at P2 it flows till Pn. Say if information starts at Pn it ends here itself.
We have two types of queries
Query 1: We have to answer where does it end if information starts at Pi?
Query 2: We may remove any existing edge, Eg we break a link say P2--> P3
Now the chain may look like P1--> P2 and P3 --> P4 -->...--> Pn now the query 1 for P1 is P2 and query1 for P2 is also P2?
I have seen this question in one contest on some website and it is removed now if you have seen something similar you can share here.
I want to know how to solve this efficiently?











Writing this on mobile, so bear with me.
There will be a single node in the tree that will have all edges incoming into it. Consider this the root of this tree.
Whenever you break an edge from this tree, you will create a forest of two trees, where the new tree is rooted at the node that the edge was broken.
If you are allowed to solve it offline, then what you can do is to solve it backward in time.
Assume that eventually all the edges are broken, and the nodes are bare. Then you can apply DSU to represent this set of rooted trees.
Every edge broken (in reverse time) becomes an unite() operation. And every "where will information flow?" query becomes a find-set() operation.
Can we do it online?
You can do it online using Tarjan's Link-Cut Trees algorithm.
You can also do it (depending on bounds) with sqrt tricks.
How can we do this? I know that there's a version of dynamic-connectivity-offline algorithm that uses sqrt-decomposition on queries, but I never heard that we can do anything similar when we have to solve the problem online. Can you please elaborate?
There's at most one edge leaving every node. A naive algorithm to solve this problem would look something like this:
Let
next[u]be the result of following the outgoing edge from u, or -1 if there is no outgoing edge. To answer a query, do something likeDeleting an edge would just be setting next[u] to -1.
Obviously the while loop above would take O(n) time. However, we can do better by batching up our calls to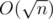 times. Now simulating the while loop above takes
times. Now simulating the while loop above takes 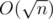 time, and when deleting an edge, there are at most
time, and when deleting an edge, there are at most 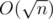 entries in
entries in 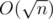 .
.
next. Keepnextas is, but also keep another array, maybe calledjump, which stores the result of callingnextjump, so both deletions and updates areSee I didn't understand why there will be only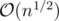 operations when we update, it is not always a chain, and there is no indexing so which jump we have to update? And what jumps do we have to store? Does jump store an element for each element?
operations when we update, it is not always a chain, and there is no indexing so which jump we have to update? And what jumps do we have to store? Does jump store an element for each element?
Can you please explain for this Image?
If edges are only deleted, not added, then we may use a parallel traversal technique.
When we remove an edge (u, v), we start BFS (or non-recursive DFS) from u and v in parallel. We run the following loop: on each iteration, find exactly one new vertex belonging to u's component and exactly one new vertex belonging to v's component. When one of the components is fully traversed, we may recolor it with another DFS or BFS, and just stop traversing the second component. This way, we delete each edge in O(min(su, sv)), where su and sv are the sizes of the resulting components, respectively. The whole process will run in amortized, because it's almost the same as small-to-large merging technique (just backwards).
amortized, because it's almost the same as small-to-large merging technique (just backwards).
This should be implemented carefully. We should avoid processing too much vertices in each component. For example, if on each iteration we extract a vertex from stack/queue (depending on the algorithm you use) and iterate over all its neighbours, this may result in TL since we may process too many vertices from the component. Instead, we should find exactly one new neighbour of the vertex we extracted from the stack, for example, by keeping track of the last edge we processed for each vertex.
All of this can be tricky to implement. We once solved a problem requiring this technique, here's the code we got (the function step is the most important here, it actually implements picking no more than one additional vertex from a component). I hope this code's right, we got AC with it :D
A (maybe) cleaner way to implement parallel traversal is to not do it in parallel at all. Run the traversals sequentially, but impose a certain limit of vertices they can visit before stopping. If both traversals reach the limit, double the limit and run them again. At some point, one of them will stop earlier than the set limit and you know you've found the smaller component and the complexity will still be linear in its size.
That's a cool trick! Never thought about applying "binary lifting" in this problem.
One interesting thing about it is that even if we start iterating on neighbours of the first vertex in the queue from the beginning of its adjacency list (not from the last visited vertex), it will still be because if the previous limit was k, then we won't skip more than k vertices because of it. And that essentially just doubles the runtime.
because if the previous limit was k, then we won't skip more than k vertices because of it. And that essentially just doubles the runtime.
However, we still need to check if we found enough vertices in each component each time we push a vertex into the stack/queue.
Can't we just map the nodes to their indexes and then when we have a query of the second type eg: edge between p3 and p4 just put p3 in a set and when we have a query of the first type eg: node p2 our answer will be the lower_bound of p2 in our set? Of course we will have to put pN in the set before we start.
I think your approach will work only if the tree is like chain, but the queries are on any directed tree with atmax one outgoing edge from a vertex. For example if the tree is in the shape of Y, can you please share your indexing?
Ah sorry I'm mistaken. I thought that the tree can only be a chain. That's why I was so confused about why is everyone not mentioning this solution. Sorry to waste your time.