Recently i got a task from my teacher: Given two numbers n and m(10^10<=n<=10^11. 1<=m<=10^5) Find all prime numbers in range [n, n + m].
1 sec, 32 mb
Help plz
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 166 |
| 2 | maomao90 | 163 |
| 2 | Um_nik | 163 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | nor | 153 |
| 9 | Dominater069 | 153 |
Recently i got a task from my teacher: Given two numbers n and m(10^10<=n<=10^11. 1<=m<=10^5) Find all prime numbers in range [n, n + m].
1 sec, 32 mb
Help plz
| Название |
|---|



Use segmented sieve, here's a nice tutorial on it: https://forthright48.com/2015/09/segmented-sieve-of-eratosthenes.html
Note that if an integer x in the range [n, n + m] is non-prime, than it should be divisible by some prime number p ≤ P, where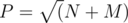 , N = 1011 and M = 105. Hence, the required numbers may be found by excluding all non-prime numbers in this range. The performance of the solution may be improved by observing that all the required numbers are odd numbers. A non-prime odd number is the product of two odd numbers.
, N = 1011 and M = 105. Hence, the required numbers may be found by excluding all non-prime numbers in this range. The performance of the solution may be improved by observing that all the required numbers are odd numbers. A non-prime odd number is the product of two odd numbers.