tumaryuido's blog

Big prime numbers

By tumaryuido, history, 6 years ago, In English

Recently i got a task from my teacher: Given two numbers n and m(10^10<=n<=10^11. 1<=m<=10^5) Find all prime numbers in range [n, n + m].

1 sec, 32 mb

Help plz

  • Vote: I like it
  • 0
  • Vote: I do not like it

»
6 years ago, # |
  Vote: I like it +11 Vote: I do not like it

Use segmented sieve, here's a nice tutorial on it: https://forthright48.com/2015/09/segmented-sieve-of-eratosthenes.html

→ Reply
»
6 years ago, # |
← Rev. 5   Vote: I like it +3 Vote: I do not like it

Note that if an integer x in the range [n, n + m] is non-prime, than it should be divisible by some prime number p ≤ P, where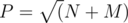 , N = 1011 and M = 105. Hence, the required numbers may be found by excluding all non-prime numbers in this range. The performance of the solution may be improved by observing that all the required numbers are odd numbers. A non-prime odd number is the product of two odd numbers.

→ Reply