Given a list rectangles [R1, R2, R3] defined by their lower left and upper right [(x1, y1), (x2, y2)] coordinates, and a value k.
Is there an optimal way to find area where k rectangles overlap?
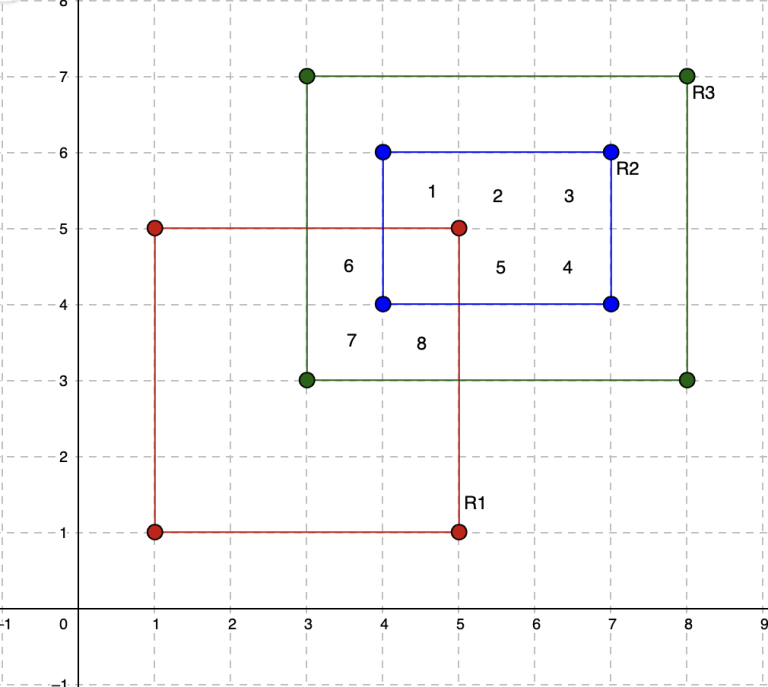
For example:
R1: [(1, 1), (5, 5)]
R2: [(4, 4), (7, 6)]
R3: [(3, 3), (8, 7)]
rectangles = [R1, R2, R3]
k = 2
The area which is overlapped by two rectangles is 8.
If the coordinates are small enough (say, |x|, |y| <= 5000) you can use lazy update in RSQ 2D table. So, if you have N rectangles, X = width of board, Y = height of board, the complexity is O(1) for each lazy update, and the actual updating takes O(X*Y) so total complexity is O(N+X*Y) and then you count how many cells have value = K. If you need solution for bigger X and Y you should try with sweep line, but don't really know how.
There is a sweep line solution to compute the area covered by the intersection of exactly two rectangles among n rectangles.
We sort all events, each containing {x, y1, y2, type}, by the x coordinate, where [y1, y2] represents the range of active segments and type indicates whether it is an opening or closing event. Let T1 be the segment tree that maintains the total length covered by at least one rectangle, T2 for at least two rectangles, and T3 for at least three.
The contribution to the answer at the i-th event is
(event[i+1].x − event[i].x) * (T2[1] − T3[1])However, I don’t quite understand this idea. Sometimes a node in the segment tree T2 doesn’t actually represent the true length covered by at least two rectangles, yet T2[1] still gives the correct total value as desired
https://ideone.com/JZg2EZ
To find area where k rectangles overlap, I think the solution is similar.