Разбор задачи "E. Хитрый и умный пароль"

Общая схема решения

Общая схема авторского решения следующая. Переберём позицию pos центра средней части middle ответа (той, которая является палиндромом). Дальше возьмём в качестве middle максимальный подпалиндром, имеющий середину ровно в позиции pos. После этого надо взять в качестве prefix и suffix такие максимальные по длине строки, что они удовлетворяют всем условиям задачи, и при этом не пересекаются с выбранной серединой.

Выполнив эту процедуру для каждой позиции pos и выбрав среди всех найденных ответов наилучший, - получим ответ на задачу.

Реализация

Фактически, задача состоит из двух подзадач:

Во-первых, определение максимальной длины палиндрома, имеющего центр в заданной позиции. Это делается за O(n) алгоритмом, описанным у меня на сайте. Иначе это можно делать с помощью бинпоиска и, например, хешей: переберём бинарным поиском эту самую искомую длину палиндрома, а внутри бинпоиска сравнивать две строки на равенство легко можно с помощью хешей (надо только посчитать два массива хешей для строки, и для её разворота).

Во-вторых, это определение длин и позиций максимальных частей prefix и suffix, не пересекающихся с заданной подстрокой [l;r]. Заметим, что если мы будем рассматривать все длины sufflen суффикса suffix в порядке увеличения, то для каждой такой длины sufflen в качестве prefix будет выгодно брать самое левое вхождение строки prefix = reverse(suffix). Таким образом, увеличивая длину suffix, мы можем сдвинуть prefix только вправо, но не влево. Обозначив через lpos[sufflen] эту самую позицию самого первого вхождения строки reverse(suffix(sufflen)), получаем, что эти lpos являются неубывающими величинами. Введём для удобства ещё величину rpos[len] = lpos[len] + len - 1 - позицию окончания вхождения этого суффикса (эти величины уже строго возрастают, как легко понять).

Итак, если бы мы знали значения этого массива lpos (а ещё удобнее - rpos), то в решении общей задачи (там, где после выбора максимального в pos палиндрома мы искали максимальные подходящие prefix и suffix) можно использовать бинарный поиск по длине sufflen (или просто предпосчитать заранее ответы на всевозможные запросы - тогда ответ на запрос будет за O(1)).

Осталось научиться считать массив lpos позиций вхождений ревёрснутых суффиксов.

Например, можно это делать хешами: пусть мы посчитали lpos[k], научимся считать lpos[k + 1]. Если строка s.substr(lpos[k], k + 1) совпадает с суффиксом длины k + 1, то lpos[k + 1] = lpos[k]. В противном случае, пробуем увеличить lpos[k + 1] на единицу, и снова выполняем сравнение, и т.д. Сравнение подстрок можно делать за O(1) с помощью хешей. И понятно, что в сумме тогда на построение всего массива уйдёт O(n) - ведь мы не могли совершить продвижений указателя вправо более, чем n раз.

Другой способ построения массива lpos, более "чёткий" - использовать префикс-функцию. Для этого сделаем строку reverse(s) + # + s, ну и просто в тех точках в правой половине полученной строки префикс-функция приняла значение k, поставить lpos[k] =  этой позиции (если, конечно, lpos[k] ещё не было присвоено какому-то другому значению - нам ведь надо искать самое первое вхождение).

Итак, в итоге довольно легко получить решение этой задачи за O(n) с помощью двух довольно известных подходов: массива палиндромностей за O(n) (алгоритм, кстати, сильно похожий на алгоритм вычисления z-функции), и хеши либо префикс-функция. Решение за можно было собрать вообще из одних хешей: ища максимальные палиндромы с помощью бинпоиска, и ища sufflen тоже с помощью бинпоиска по вычисленному хешами массиву rpos.

Доказательство

Единственный неочевидный момент - почему при фиксированной pos - позиции середины центрального элемента middle - можно жадно брать максимальный палиндром с центром в ней.

Предположим противное: выгодно было брать не максимальный палиндром pal, а какой-то меньше. Посмотрим, что происходит, когда мы уменьшаем pal на единицу. Тогда длина средней части middle уменьшается на два, но зато увеличивается "свобода" для prefix и suffix. Но для каждого из них "свобода" увеличилась только на единицу: для prefix стал доступен один символ в конце, а для suffix - в начале. Значит, самое лучшее, что могло произойти, - это увеличение длины suffix на один (здесь мы пользуемся монотонностью rpos). Следовательно, при переходе от pal к pal - 1 мы потеряли два символа в длине middle, и могли выиграть максимум два символа в suffix и prefix. Значит, это уменьшение никогда не выгодно.

Другой подход к решению

Рассмотрим здесь другой способ решения этой задачи, который использовался многими участниками на контесте.

Давайте пойдём к решению с другой стороны: будем перебирать не позицию middle, а длину prefix и suffix. Теперь при фиксированных суффиксе и префиксе мы должны найти наибольший палиндром между ними, и не пересекающийся с ними.

Следует отметить, что жадность, похожая на предыдущее решение, не верна: выбрать максимальный палиндром с центром между prefix и suffix, и "обрезать" его так, чтобы он не налазил на prefix и suffix. Она неверна, потому что может быть было выгодно взять исходно не самый большой палиндром в промежутке между префиксом и суффиксом, но он станет самым выгодным после "обрезания".

Таким образом, при фиксированных префиксе и суффиксе (кстати, чтобы их зафиксировать, надо использовать какой-то из методов, описанных в предыдущем алгоритме) наша задача - научиться делать максимум в массиве палиндромностей "с обрезанием". Это значит, что поступает запрос вида "найти максимальный палиндром, целиком лежащий в отрезке [l;r]", и мы должны среди всех позиций i = l... r выбрать ту, которая даёт наибольший палиндром с центром в ней, т.е. максимизирует min(pal[i], min(r - i, i - l)). Ответить на такой запрос можно например следующим образом: будем искать искомую длину палиндрома бинарным поиском. Пусть x - фиксированная длина палиндрома внутри бинарного поиска, мы хотим проверить, есть ли такой палиндром или нет. Для этого надо проверить, есть ли на отрезке [l + x;r - x] хотя бы одно число, больше либо равное x, - а это можно сделать с помощью дерева отрезков, построенного над предварительно вычисленным массивом палиндромностей pal (как строить его эффективно, тоже описано в предыдущем алгоритме).

Тогда асимптотика решения будет 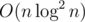, хотя её можно уменьшить до 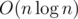, заменив дерево отрезков sparse-table (это когда для каждой позиции i и каждой степени двойки j предпосчитывают ответ на отрезке [i;i + j - 1]).