Codeforces Round #585 Editorial

#	User	Rating
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

#	User	Contrib.
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

Editorial

Solution (fcspartakm)

#include <bits/stdc++.h>

using namespace std;

int a1, a2, k1, k2, n;

inline void read() {
	cin >> a1 >> a2 >> k1 >> k2 >> n;	
}

inline void solve() {
	if (k1 > k2) {
		swap(k1, k2);
		swap(a1, a2);
	}
	int minCnt = max(0, n &mdash; a1 * (k1 &mdash; 1) &mdash; a2 * (k2 &mdash; 1));
	int maxCnt = 0;
	if (n <= a1 * k1) {
		maxCnt = n / k1;
	} else {
		maxCnt = a1 + (n &mdash; a1 * k1) / k2;
    }    
    cout << minCnt << ' ' << maxCnt << endl;
}

int main () {
#ifdef fcspartakm
    freopen("input.txt", "r", stdin);
    //freopen("output.txt", "w", stdout);
#endif
    srand(time(NULL));
    cerr << setprecision(10) << fixed;
    
    read();
    solve();
 
    //cerr << "TIME: " << clock() << endl;
}

1215B - The Number of Products

Editorial

Solution (fcspartakm)

#include <bits/stdc++.h>

using namespace std;

const int N = 200 * 1000 + 13;

int n;
int a[N];

inline void read() {	
	cin >> n;
	for (int i = 0; i < n; i++) {
		cin >> a[i];
	}
}

inline void solve() {
	int pos = -1;
	li ans0 = 0;
	for (int i = 0; i < n; i++) {
		if (a[i] == 0) {
			pos = i;
		}
		if (pos != -1) {
			ans0 += pos + 1;
		}
	}	
	int cnt1 = 0, cnt2 = 0;
	int bal = 0;
	li ansP = 0;
	for (int i = 0; i < n; i++) {
		if (a[i] == 0) {
			cnt1 = 0, cnt2 = 0, bal = 0;
			continue;
		}
		if (bal % 2 == 0) {	
			cnt1++;
		} else {
			cnt2++;
		}
		if (a[i] < 0) {
			bal++;
		}
		if (bal % 2 == 0) {
			ansP += cnt1;
		} else {
			ansP += cnt2;
		}
	}
	cout << n * 1ll * (n + 1) / 2 - ans0 - ansP << ' ' << ansP << endl;
}

int main () {
#ifdef fcspartakm
    freopen("input.txt", "r", stdin);
    //freopen("output.txt", "w", stdout);
#endif
    srand(time(NULL));
    cerr << setprecision(10) << fixed;
    
    read();
    solve();
 
    //cerr << "TIME: " << clock() << endl;
}

1215C - Swap Letters

Editorial

Solution (fcspartakm)

#include<bits/stdc++.h>

using namespace std;

int n;
string s, t;

inline void read() {	
	cin >> n >> s >> t;
}

inline void solve() {
	vector<int> pos01, pos10;
	for (int i = 0; i < n; i++) {
		if (s[i] != t[i]) {
			if (s[i] == 'a') {
				pos01.pb(i);
			} else {
				pos10.pb(i);
			}
		}
	}
	if (sz(pos01) % 2 != sz(pos10) % 2) {
		cout << -1 << endl;
		return;
	}
	vector<pair<int, int> > ans;
	for (int i = 0; i + 1 < sz(pos01); i += 2) {
		ans.pb(mp(pos01[i], pos01[i + 1]));
	}
	for (int i = 0; i + 1 < sz(pos10); i += 2) {
		ans.pb(mp(pos10[i], pos10[i + 1]));
	}
	if (sz(pos01) % 2) {
		int x = pos01.back();
		int y = pos10.back();
		ans.pb(mp(x, x));
		ans.pb(mp(x, y));
	}
	cout << sz(ans) << endl;
	for (int i = 0; i < sz(ans); i++) {
		cout << ans[i].ft + 1 << ' ' << ans[i].sc + 1 << endl;
	}
}

int main () {
#ifdef fcspartakm
    freopen("input.txt", "r", stdin);
    //freopen("output.txt", "w", stdout);
#endif
    srand(time(NULL));
    cerr << setprecision(10) << fixed;
    
    read();
    solve();
 
    //cerr << "TIME: " << clock() << endl;
}

1215D - Ticket Game

Editorial

Solution (fcspartakm)

#include <iostream>
#include <set>
#include <string>
#include <vector>
#include <algorithm>
#include <cmath>

using namespace std;

int n;

int main() {
    cin >> n;
    long double sum1 = 0, sum2 = 0;
    string s;
    cin >> s;
    for (int i = 0; i < n; i++) {
        if (s[i] != '?') {
            if (i < n / 2) {
                sum1 += (long double)(s[i] - '0');
            } else {
                sum2 += (long double)(s[i] - '0');
            }
        } else {
            if (i < n / 2) {
                sum1 += (long double)4.5;
            } else {
                sum2 += (long double)4.5;   
            }
        }
    }
    if (fabsl(sum1 - sum2) < 1e-9) {
        cout << "Bicarp" << endl;
    } else {
        cout << "Monocarp" << endl;
    }
}

1215E - Marbles

Editorial

Solution (fcspartakm)

#include <iostream>
#include <set>
#include <string>
#include <vector>
#include <algorithm>

using namespace std;

const int N = 1000 * 1000 + 13;
const int M = 20 + 1;
const long long INF = 1000 * 1000 * 1000 * 1ll * 1000 * 1000 * 1000;

int n;
long long d[(1 << M)];
long long cnt[M][M];
vector<int> col[M];

int main() {
    cin >> n;
    for (int i = 0; i < n; i++) {
        int x;
        cin >> x;
        x--;
        col[x].push_back(i);
    }
    for (int i = 0; i < 20; i++) {
        for (int j = 0; j < 20; j++) {
            if (i == j) {
                continue;
            }
            if ((int)col[i].size() == 0 || (int)col[j].size() == 0) {
                continue;
            }
            int pos2 = 0;
            for (int pos1 = 0; pos1 < (int)col[i].size(); pos1++) {
                while (true) {
                    if (pos2 == (int)col[j].size() - 1 || col[j][pos2 + 1] > col[i][pos1]) {
                        break;
                    }
                    pos2++;
                }
                if (col[i][pos1] > col[j][pos2]) {
                    cnt[i][j] += pos2 + 1;
                }
            }
        }
    }

    for (int mask = 0; mask < (1 << 20); mask++) {
        d[mask] = INF;
    }
    d[0] = 0;
    for (int mask = 0; mask < (1 << 20); mask++) {
        vector<int> was;
        for (int i = 0; i < 20; i++) {
            if (mask & (1 << i)) {
                was.push_back(i);
            }
        }
        for (int i = 0; i < 20; i++) {
            if (mask & (1 << i)) {
                continue;
            }
            long long sum = 0;
            for (int j = 0; j < (int)was.size(); j++) {
                sum += cnt[was[j]][i];
            }
            int nmask = mask | (1 << i);
            d[nmask] = min(d[nmask], d[mask] + sum);
        }
    }
    cout << d[(1 << 20) - 1] << endl;
}

1215F - Radio Stations

Editorial

Solution (BledDest)

#include<bits/stdc++.h>

using namespace std;

const int N = 1600043;

vector<int> g[N];
vector<int> gt[N];
int used[N];
vector<int> order;
int comp[N];
vector<int> result;
int v;

void add_edge(int v1, int v2)
{
	g[v1].push_back(v2);
	gt[v2].push_back(v1);
}

void add_disjunction(int v1, int v2)
{
	add_edge(v1 ^ 1, v2);
	add_edge(v2 ^ 1, v1);
}

void dfs1(int v)
{
	if(used[v]) return;
	used[v] = 1;
	for(auto u : g[v])
		dfs1(u);
	order.push_back(v);
}

void dfs2(int v, int cc)
{
	if(comp[v]) return;
	comp[v] = cc;
	for(auto u : gt[v])
		dfs2(u, cc);
}

bool solve2SAT()
{
	for(int i = 0; i < v * 2; i++)
		dfs1(i);
	reverse(order.begin(), order.end());
	int cc = 0;
	for(auto x : order)
	{
		if(comp[x] == 0)
		{
			cc++;
			dfs2(x, cc);
		}
	}
	for(int i = 0; i < v; i++)
	{
		if(comp[i * 2] == comp[i * 2 + 1])
			return false;
		else if(comp[i * 2] > comp[i * 2 + 1])
			result.push_back(i);
	}
	return true;
}

int main()
{
	int n, p, M, m;
	scanf("%d %d %d %d", &n, &p, &M, &m);
	v = p + M - 1;
	for(int i = 0; i < n; i++)
	{
		int x, y;
		scanf("%d %d", &x, &y);
		--x;
		--y;
		add_disjunction(x * 2, y * 2);
	}
	for(int i = 0; i < p; i++)
	{
		int l, r;
		scanf("%d %d", &l, &r);
		if(l != 1)
			add_disjunction((l - 2 + p) * 2, i * 2 + 1);
		if(r != M)
			add_disjunction((r - 1 + p) * 2 + 1, i * 2 + 1);
	}
	for(int i = 0; i < m; i++)
	{
		int x, y;
		scanf("%d %d", &x, &y);
		--x;
		--y;
		add_disjunction(x * 2 + 1, y * 2 + 1);
	}
	for(int i = 2; i <= M - 1; i++)
	{
	    int f1 = i - 2 + p;
	    int f2 = f1 + 1;
	    add_disjunction(f1 * 2, f2 * 2 + 1);
	}
	if(!solve2SAT())
	{
		puts("-1");
		return 0;
	}
	int k = 1;
	vector<int> stations;
	for(auto x : result)
		if(x < p)
			stations.push_back(x);
		else
			k = max(k, x - p + 2);
	printf("%d %d\n", int(stations.size()), k);
	for(auto x : stations)
		printf("%d ", x + 1);
	return 0;
}

+-+-+ Then he is increasing pos whenever curr is +; initially, curr = 1, pos = 1; (*) + ->curr = 1, pos = 2; (*) - ->curr = -1, pos = 2; + ->curr = -1, pos = 2; - ->curr = 1, pos = 3; (*) + ->curr = 1, pos = 4; (*) Therefore, neg = 5+1 - pos = 2;

Comments (63)

Show archived | Write comment?

AliShahali1382

5 years ago, # |

F was Perfect!!

→ Reply

mohamedeltair

+77

Another proof for $$$D$$$:

Consider first the cases where there are question marks only in one side, assume their count is $$$C$$$ ($$$C$$$ is $$$even$$$). Let the side without question marks be $$$S_1$$$ and the other side be $$$S_2$$$, and let $$$Sum(S_1)-Sum(S_2)$$$ be $$$d$$$:

$$$Case_1$$$ ($$$d=\dfrac{C}{2}*9$$$): When Monocarp puts $$$x$$$, Bicarp puts $$$9-x$$$, and Bicarp wins.
$$$Case_2$$$ ($$$d>\dfrac{C}{2}*9$$$): Monocarp always puts $$$0$$$, so $$$d$$$ will always be $$$>0$$$, and Monocarp wins.
$$$Case_3$$$ ($$$d<\dfrac{C}{2}*9$$$): Monocarp always puts $$$9$$$, so $$$d$$$ will be $$$<0$$$ at the end, and Monocarp wins.

Now consider the cases where there are question marks in both sides. Let the side with less question marks be $$$S_1$$$ and the other side be $$$S_2$$$, and let $$$Sum(S_1)-Sum(S_2)$$$ be $$$d$$$. Assume $$$S_1$$$ has $$$C_1$$$ question marks and $$$S_2$$$ has $$$C_2$$$ question marks ($$$C_1+C_2$$$ is $$$even$$$), and let $$$C$$$ be $$$C_2-C_1$$$:

If $$$d=\dfrac{C}{2}*9$$$: When Monocarp puts $$$x$$$ in one side, Bicarp puts $$$x$$$ in the other side. Thus $$$d$$$ never changes, and we reach $$$Case_1$$$.
If $$$d>\dfrac{C}{2}*9$$$: Monocarp first puts $$$9$$$ in $$$S_1$$$. And when Bicarp puts $$$x$$$ in one side, Monocarp puts $$$x$$$ in the other side, until $$$odd$$$ number of question marks remain in $$$S_2$$$. At this point, $$$d>\dfrac{C}{2}*9+9$$$. So after Bicarps's turn, $$$d$$$ must be $$$>\dfrac{C}{2}*9$$$ and we reach $$$Case_2$$$.
If $$$d<\dfrac{C}{2}*9$$$: Monocarp first puts $$$0$$$ in $$$S_1$$$. And when Bicarp puts $$$x$$$ in one side, Monocarp puts $$$x$$$ in the other side, until $$$odd$$$ number of question marks remain in $$$S_2$$$. At this point, $$$d<\dfrac{C}{2}*9$$$. So after Bicarps's turn, $$$d$$$ still must be $$$<\dfrac{C}{2}*9$$$ and we reach $$$Case_3$$$.

SLIMSHADYNICK

4 years ago, # ^ |

God level explanation!

Aqour

ypa

CKang

In Problem B

the input is

The second line contains n integers $$$a_1,a_2,…,a_n (−10^9≤a_i≤10_9;a_i≠0)$$$ — the elements of the sequence.

but the Tutorial with many

if(a[i]==0)

why ?

jjang36524

5 years ago, # ^ |

That's just for input error or testcase error

xsanchez

I think he just considered a[i] == 0 case too. But as given in question there are no element with 0 value so we can just skip this condition , rest of the solution is same .

Yash_Jain

This is my code for D which simulates the game optimally .My Code

Beso.Managadze

-9

Nice solution!

keleven

60628371 Here is my code and I wanna know why the runtime error

for problem B

0f_0b

The write to arr[(n << 1)] on line 18 caused array index overflow.

Increasing the size of the array seems to work.

 	long ans[2];
 	cin >> n;
 	//vector<long> arr(n << 1);
-	long *arr = new long[(n << 1)];
+	long *arr = new long[(n << 1) + 1];
 	cin >> next;
 	if (next > 0) {
 		ans[0] = arr[0] = 1;

woshinande

← Rev. 2 →

+21

I have some questions for E:

When we place all marbles of type i in front of all marbles of type j, the relative positions between type i and other types can change. So when we do transition in the dp state, how can we ensure that summing up all cnt[j][i] is the number of extra moves that we need?
Say we need to add marble i to dp[mask], after we move all the marbles in mask to the front of type i, the positions of all the marbles in mask is potentially scrumbled. In that case, how is dp[mask] still the number of moves needed to reorder the marbles in mask after moving them to the front of type i marbles? For example, say the order is {2, 3, 1, 2}. When we move all type 1 and 2 marbles to the front of type 3, the number of moves needed to reordred type 1 and 2 is from state {2, 1, 2, 3}, and is different from reordering them from state {2, 3, 1, 2}, which is the initial state.

Hope my questions make sense.

+17

For those of you who are as confused as I was, I asked my friend who ACed this problem and the explaination is as follow:

When we transit from one dp state to another, we only consider types that are in the mask. So when we try to place type i as the last marbles in this dp state, each swap of type i marble with the other marbles is counted in cnt[j][i], for some j in the mask. So the summation of cnt[j][i] is indeed the number of extra steps that we need to take.
The cue to understand the dp state properly is to know that dp[mask] means we only consider marbles that are in the mask and ignore other types. Take the same example {2, 3, 1, 2} here. Say we wanna transit from dp[011] to dp[111] (adding type 3 marbles), and want the last marbles to be of type 3. dp[011] means the number of steps needed to reorder {2, 1, 2}, as we ignore type 3 marbles. Thus dp[111] equals to summation of cnt[j][3] + dp[011].

I hope this explanation helps.

vinayak_jha226

can you make me understand why does cnt[j][i] is indeed the number of swaps required. because as far as i know in the mask the positions of the 1s' in the mask have already changed. And the precalculated cnt[j][i] will then remain invalid. Where is the flaw in my reasoning??

cnt[j][i] would only factor in the relative positions between type i and j. i.e. only the swaps between type i and j are counted, swaps between type i and another type k would be taken care of in cnt[k][i], and so is the case between type j and type k.

When you try to move type j marbles in front of all the marbles in mask, each swap would be counted only once in cnt[j][i], for some i in the mask, because we only consider type j and types that are in the mask.

Hope the explanation helps.

Correct me if i am wrong this then means, that when bit i is moved ahead of all bits marked 1 in mask then later on when the bit k is added is already taken care of despite the change in positions or in other words cnt[i][k] when added already takes care of bits that are marked 1.

It's not proper for you to think that way because $$$dp[mask]$$$ only means types in mask is "sorted" in some order, not necessarily means type i is at the very beginning. We don't really have to care about the order of how it is "sorted".

Maybe it's better to think of the dp transition this way: when you try to "sort" all marbles of type k and types in mask, one way you can do is to put all types in mask in front of type k, this is what $$$\sum_j^{j\in mask} cnt[j][k]$$$ accounts for. Then you "sort" all the marbles that are in mask, which is what $$$dp[mask]$$$ accounts for. You sum these two terms up to get $$$dp[mask|1«k]$$$ under this configuration.

Sorry if I am being very stupid,if the mask elements are already sorted, then isn't it possible that cnt[j][i], doesn't give the right value to add to the dp transition.I mean to say if you are swapping then don't you have to swap types of colour not in the mask . How are they accounted for?

Swaps involving types not in mask will be accounted in a later stage where that type is being considered in the state transition

AjaySabarish

This is the beauty of this solution, though "it may seem" the elements in mask have gone left, we haven't paid the entire cost! In the sense while moving to the left, the mask elements may have crossed some non-mask elements also, that should have costed some swaps but we never paid it, now for adding color j into the mask, already present mask elements must go left,from the intitial point they may have travelled some crossing j due to earlier added mask elements, but we never paid that before, and now the mask elements have to go further left, so we have 2 debts to settle,i.e cost for all the mask elements should go from intitial position to complete left of j, i.e all i belonging to mask should go to left of j and by definition that is sigma(cnt[i][j]).

If we take an example : 3 2 4 3. Say we first add 4 to mask, we don't have to pay anything, now let us add 3 to mask the scenario becomes 4 3 2 3, and we have to pay 1, i.e. cnt[4][3], but if you observe we never paid for crossing 2,because we are paying only for elements in the mask. Now let us add 2 to the mask, we are paying cnt[3][2] + cnt[4][2], the total sum is cnt[4][3]+cnt[4][2]+cnt[3][2], we are paying the total cost in installments in different transitions. In short, say a color i, comes to the very front, the cost is cnt[i][1]+cnt[i][2]... ,but in one transition we pay for each element in the mask to cross the newly added element only, but when later adding another element to the mask we pay for that too!

navneet.h

solution for B. easier way is to build prefix function with 1 and -1 and calculate how many pair give positive multiplication,i.e, count[1]C2+count[-1]C2. let the number of pairs be X,then nC2 — X will be ans for negative.

BobTheBuiler

Why you initialized pos=1 ?

i am assuming 1 beforehand and considering n+1 elements,u could see that for prefix conventions if p[r]*p[l-1] denotes the sign of segment [l,r].so for 0 u need something before it.

VietCT

Can you explain me why you can caculate the number of pos subsegment by (pos*(pos-1))/2+(neg*(neg-1))/2;

ritik_patel05

consider we have a sequence like this

Notice the (*) denotes all the indexes where the curr == 1, Now see that on choosing any indexes from all the (*) and forming a segment of it will form a positive segment

Example here (*) = {0,1, 4,5} choosing (l,r] as subsegment of these indices will give you positive segment. Number of ways = (pos)C2;

Now, similarly you can see why he is adding negative count as (neg)C2;

Wow, beautiful solution brother

nonatomicgames

← Rev. 3 →

Sorry, I'm incorrectly understand Um_nik's solution:

60611022

But it's great)

g.raju2000

Hello, Can anyone explain me solution of problem C I'm not able to see why it should be proceeded this way! Thank you so much!

Edit: Sorry for this comment — I understood what was happening, Could anyone tell if I can delete this comment.Thank you!

Harshit_Pradhan

In problem B > editorial No. of subsegments should be n*(n+1)/2

CP_Sucks

Whoa editorial for D is so hard to interpret. I did in a easy way. See in left side what's the max value u can get it will be (number of ?/2)*9 + (?%2)*9 if monocarp wants to make it max and for min we calculate (number of ?/2)*9

Now do this for 2nd array also.

If maxl == maxr and minl == minr answer is bicarp coz bicarp can adjust accordingly else answer is monocarp

My submission https://mirror.codeforces.com/contest/1215/submission/60683863

Legend_of_Azkaban

whoa... just briliiant. Thanks for sharing.

How did you interpret the equation of maxvalue on each side to be (number of ?/2)*9 + (?%2)*9 ??

Greedily, so suppose monocarp try to make the left side max he will get one more chance than bicarp to do so. so if it's odd he will get the last chance to increase it. Same goes for bicarp. If suppose monocarp tries to increase left bicarp will get one more chance to increase right side. And then after the ? is finish on either side bicarp will start minimizing the other side. It just works lol. Also upvote if u find it helpful :p

So you are saying that Monocarp will try to increase the sum of one side by changing '?' into 9, and bicarp will change '?' on the same side into 0. So Monocarp has at most (number of '?' on that side)/2 chances and then +1 if the number of '?' is odd. But though your solution is fairly simple but it is hard to see why this actually "works"...

In problem D, my thought was to first divide the array in two halves (namely left and right). Then calculate the cumulative sum in both sides (suml and sumr) considering any '?' = 0. Then Monocarp will pick the side where the cumulative sum is larger and put 9 in place of '?' and try to make this side even larger. And then (if he has more moves) he would try to put 0 on the other side to prevent bicarp from catching up. So after that if the side with "less sum to start with" becomes greater or equal than the other side that means bicarp can successfully catch up. But I am getting wrong answer at test case 23: https://mirror.codeforces.com/contest/1215/submission/60690503 Please point out where I am going wrong.

+11

Solution of D in simple terms:

Because the size of the array(lets call it array for simplicity) in input is EVEN, we can always divide this array into two equal parts. Then for bicarp to win he must make sure the two parts have equal sum.

So first of all we will find the sum of the left side of the array() "lsum" and we will find the sum of the right side of the array "rsum" (consider '?' as 0). Now there are 3 cases — 1) lsum == rsum , 2) lsum > rsum 3) lsum < rsum.

Now we will use the '?' marks in both sides and try to make both sides equal so that bicarp wins. But if Monocarp has some strategy such that he always prevents bicarp from doing so then Monocarp wins.

1) Lets consider lsum == rsum:: If there are equal number of '?' on both sides Bicarp can nullify any moves of Monocarp and keep the two sides equal. If monocarp changes one '?' into X on any side, bicarp can change one '?' on the other side into X, so both sides remain the same. As there are equal number of '?' in both sides, bicarp can always do the same.

Now if there are unequal number of '?' on both side, then one side will have more '?' than the other side but the initial sum is equal on both sides(as we assumed for now). In that case Monocarp can choose the side with more '?' and keep changing them into 9 so that the sum of this side gets bigger and bigger. To keep things equal bicarp must keep changing '?' marks on the other side by 9. But as Monocarp's side has more '?' (at least two more than bicarp's side, because the number of '?' is even), bicarp will eventually run out of '?' on his side, but there will AT LEAST be 2 '?' on Monocarp's side. So Monocarp can change one of these into 9 , now even if bicarp chooses 0(lowest) for the other '?' , Monocarp wins. (If instead of keeping things balanced, bicarp chose to change '?' into 0 on Monocarp's side to lessen the difference between two sides, then when Monocarp's side has no '?' left, Monocarp will start making bicarp's '?' into 0 so that bicarp cannot catch up with Monocarp's side, and as there is already less '?' in bicarp's side, bicarp stands no chance.)

Now that we realize there is a connection of number of '?' on each side with our solution let's denote lcnt = (number of '?' on left side) and rcnt = (number of '?' in right side).

2) Now consider that lsum > rsum && lcnt > rcnt , we have one side with more sum (initially) and more '?' marks. So Monocarp will choose this side and keep changing '?' into 9. And bicarp will try to keep things balanced but will eventually run out of '?' and loose (by the same logic applied in 1). Same goes for (rsum > lsum && rcnt > lcnt).

3) Now consider lsum > rsum but lcnt < rcnt :: Now Monocarp will change the '?' on left side(I arbitrarilly picked the left side to have more sum but less '?', vice versa is ofc possible) into 9 to make it even larger and bicarp will do the same on the right side and not let the difference to increase (So lsum-rsum remains constant). Eventually Monocarp will run out of '?'. So bicarp has some '?' left. If he can reach lsum using these '?' then bicarp wins. So basically we do this,

sum = lsum-rsum; cnt = rcnt-lcnt;

Now before the tricky part let's make sure you understand two things: i) the very first move of the game was made by Monocarp, so after some moves if "moves by Monocarp" = "moves by Polycarp", clearly the next move will be made by Monocarp. So Monocarp will change any available '?' and bicarp has the chance to observe and move carefully. ii) Right now (after Monocarp uses all of his sides '?') Monocarp and bicarp will have equal amount of moves and equal amount of '?' to change (think about cases where Monocarp has i) EVEN or ii) ODD number of '?' at the very begining). Now the tricky part, Monocarp has two options to win, if he can overflow this side, means that if he changes all the '?' available for him (if there are 4 '?' available Monocarp can touch only 2) into 9, then even if bicarp chooses 0 for his '?', rsum becomes greater than lsum. In that case Monocarp's best choice is to use 9 for all '?'. Or if he can underflow this side, that is choose 0 for all '?' (he can touch) and thus even if bicarp chooses 9 for his '?', rsum remains less than lsum. The only way bicarp can win is if rsum + (cnt/2 * 9) = lsum, that is he needs to make all '?' on his control 9 in order to win. Why this works? If Monocarp tries to overflow and chooses 9 for one '?' bicarp can choose 0 for one of his '?'. If Monocarp chooses 0 , bicarp can choose 9. If Monocarp chooses 6, bicarp chooses 3. (notice as Monocarp moves first, bicarp can observe and choose optimally).

Code : https://mirror.codeforces.com/contest/1215/submission/60696313

memento

+10

akashtomar19

Your approach is failing at s="441???" Monocarp has more chances here he wins in every condition. But your output is Bicarp

Unfortunately you missed the last sentence of the input section which states that "The number of "?" characters is even".

adarsh000321

Can anyone provide more intuitive proof for problem D, mohamedeltair's proof was nice but i only got the 1st part of it

hitch

In C, what would the solution look like if the strings were allowed to have characters from a..z

Tathagat_shah

In C, what would the solution look like if the strings were allowed to have characters from a..z Enchom BledDest spookywooky

Thanks!

no_questions

Problem B can be done using a much simpler logic and code by iterating through the array and maintaining count of pair indices having positive product and negative product having current index as R.

NoobCoder1998

Can u pls explain ur approach in detail??

Spheniscine

← Rev. 8 →

I used a DP approach for this problem; keeping track of two values:

$$$pos_i$$$ = number of subsegments with positive product with last index $$$= i$$$
$$$neg_i$$$ = number of subsegments with negative product with last index $$$= i$$$

Transitions should be quite elementary if you think about what adding a positive/negative element would do to the product of a subsegment.

Final answer is $$$N = \sum neg$$$ and $$$P = \sum pos$$$

Code: 60664552

Sheldor.The.Conqueror

8 months ago, # ^ |

Your comment's very helpful,I was able to come up with a solution on my own after reading it.

andrewinston

Another way to think about the solution for B is:

Let $$$pos[i]$$$ be the count of sub arrays that end in i ($$$[k..i]$$$ for $$$k \geq 0$$$) whose product is positive, and $$$neg[i]$$$ the count of subarrays that end in i ($$$[k..i]$$$ for $$$k >= 0$$$) whose product is negative.

The base case for them is simple:

pos[0] = 1 if v[0] > 0, otherwise 0
neg[0] = 1 if v[0] < 0, otherwise 0

Given that $$$pos[x-1]$$$ and $$$neg[x-1]$$$ are calculated, we can easily calculate $$$pos[x]$$$ and $$$neg[x]$$$ as follows:

pos[x] = 1+pos[x-1] if v[x] > 0,
pos[x] = neg[x-1] if v[x] < 0

neg[x] = neg[x-1] if v[x] > 0,
neg[x] = 1+pos[x-1] if v[x] < 0

After these arrays are fully calculated, the amount of sub arrays that are positive is the sum of all $$$pos[i]$$$, and the amount of arrays that are negative is the sum of $$$neg[i]$$$

My submission 60721761

turik1997

What you are saying is not always true. For example, let's have an array 5, -3 Then pos[0] = 1, neg[0] = 0. neg[1] = 2, pos[1] = neg[0] + 1 = 1. But pos[1] cannot be 1 because there is no subsegment that ends at index 1 with product being positive.

Sorry, I had messed up the transitions. They're correct now. Thanks for the feedback :D

Runtime_Error97

Can you please explain your approach to this problem B

valdaarhun

Consider this example:

a = {1, 2, -2, -5, 4}

Now you have got two arrays pos[n] and neg[n]. Each of them counts the number of subarrays that end at position i and have the product of their elements as positive and negative respectively.

For the above example, pos[0] = 1 and neg[0] = 0

Now for any position i, if a[i] is negative then you will have: neg[i] = 1 + pos[i - 1] and pos[i] = neg[i - 1].

Otherwise, if a[i] is positive then: neg[i] = neg[i - 1] and pos[i] = pos[i - 1] + 1

So, in the above example you will have pos[n] = {1, 2, 0, 3, 4} and neg[i] = {0, 0, 3, 1, 1}

sparshkedia

Can anyone explain the editorial solution of E where it is calculating the number of swaps required for each pair of marbles? I didn't understand how the two pointer approach is working here.

SpargelTarzan

BledDest, Just reading and building the 2-Sat graph for F in Java gives MLE.... 60748712. It doesn't even make it to the Solve2Sat() call where there might be DFS related MLEs. Could you boost the Memory Limit?

e.m.blagov

Problem D (again... but with illustrations): Solution: https://mirror.codeforces.com/contest/1215/submission/60849161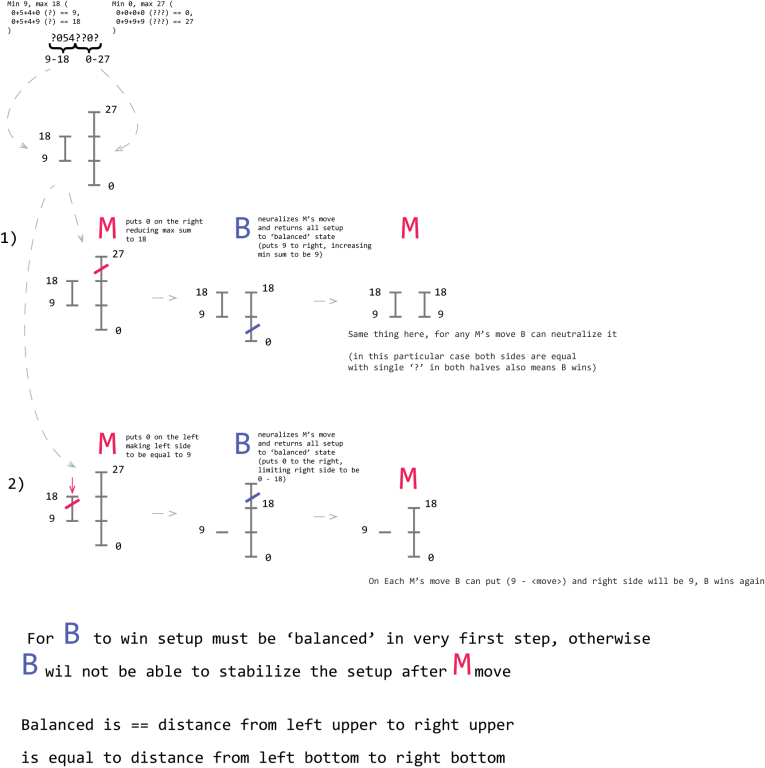

It is interesting to hear from the authors how they came up with the idea of problem D so that its solution is based on (L+R)/2 = 0. What was the order? Did you made up a problem statement after having a solution for similar problems or you built a problem and then solved it?

Why it is interesting is that I can't see any way how a person can find the property of (L+R)/2 = 0 during a competition.

BledDest

Well, initially fcspartakm proposed this problem on lower constraints, so it could be solved with dynamic programming. Then I thought about how this problem can be solved using the special structure of allowed turns (they are symmetric). I can't remember how exactly I came to the equality $$$\frac{L + R}{2} = 0$$$, but it was something like that: if the first player wants to win, they should either make the balance very low, or make it very high. So I tried to analyze these two cases (the first player wants the balance to be as low as possible or as high as possible), and then somehow arrived at this answer. I think that this formula is easier to come up with if you have mathematical background, but if you don't have it, it might be much easier to find an approach more related to programming than to maths.

I actually wanted to make this problem interactive, where the contestant should play as the second player, but, unfortunately, this was unacceptable for The Quals.

Mooncrater

Can anyone give a proof for C?

Mohammad_Yasser

4 years ago, # |

I got another way to prove D solution.

You can let each $$$?$$$ have an initial value of $$$4.5$$$, thus, on each turn, the player adds $$$x$$$ on the value of a question mark, s.t. $$$x \in [-4.5, 4.5]$$$.

That way, the second player will always be able to mirror the first player's actions.

If the first player adds $$$x$$$ to some side, the second player can add $$$-x$$$ to the same side, or add $$$x$$$ to the other side.

So if $$$ sum_{left} + 4.5 * q_{left} == sum_{right} + 4.5 * q_{right} $$$, the second player will win by mirroring.

Else, the first player will choose the larger side, and keeps increasing it, or decreasing the other one. The second player can do no better than mirroring, and will lose.

nayan6119

I think in Problem A, the checking condition for min value should be: if(n-cnt<=0)__ then min=0. In the editorial its given, cnt<=0__. Forgive me if I am wrong :)

E is one of the most beautiful solutions, I have ever seen in CP, thanks all

nishu2002

2 years ago, # |

Can anybody tell me where am I wrong in problem D? My submission 174629795

Tylee

7 weeks ago, # |

I have a much simpler solution for problem B which is using dp. First we need to for an length n array(assumen count from 1 to n),we can know the subarray of the last element in this subarray is within 1 to n.what is the meaning?For example A={1,2,3,4,5,6},{1,2,3} is a subarray for A and the position of the last element 3 in the original array A is 3 (count from 1 to n),this is a important nature. Why important?Let consider Si,Si is a subarray of A and the position of last element in Si in A is i,so we from the previous nature we know the number of subarray of A is s1+s2+s3+...+sn,so in otherword,we can know that the last element of positive/negative subarray is also within 1 to n(count from 1 to n) and it sum up is the total number of positive/negative subarray,so we can run up a dp to solve this by using below state equation dp[i][0] represent positive subarray end with i th position(count from 1 to n) element in the original array dp[i][1] represent negative subarray end with i th position(count from 1 to n) elemetn in the original array

284101755

BledDest's blog