Hey All!
Topcoder SRM 770 is scheduled to start at 12:00 UTC -4, Nov 2, 2019. Registration is now open for the SRM in the Web Arena or Applet and will close 5 minutes before the match begins.
Interested in working at Google? Well as a #TCO19 sponsor, they are looking to hire folks like you! Join us for SRM 770 to opt into their exciting job opportunities!
Thanks to jy_25, lazy_fox, idiot_owl and ashisha690 for writing the problems for the round. Also thanks to KaasanErinn and DuXSerbia for testing the problem set.
This is the third SRM of Stage 1 of TCO20 Algorithm Tournament.
Stage 1 TCO20 Points Leaderboard | Topcoder Java Applet | Next SRM 771 — Nov 27, 11:00 UTC-5
Some Important Links
| Match Results | (To access match results, rating changes, challenges, failure test cases) |
| Problem Archive | (Top access previous problems with their categories and success rates) |
| Problem Writing | (To access everything related to problem writing at Topcoder) |
| Algorithm Rankings | (To access Algorithm Rankings) |
| Editorials | (To access recent Editorials) |
Good luck to everyone!











off-topic : Algorithm Rankings is broken
Should be back up :)
is there a way to see ranking which contain users who hadn't competed in last 180 days ?
Unfortunately there no such ranking available. However you can use the advance member search and look at members in a particular range of ratings and then sort them.
For other interesting stats — you can checkout the Algorithm Record Book: https://www.topcoder.com/tc?module=Static&d1=statistics&d2=recordbook_home
Gentle Reminder: Round begins in 4 hours :)
If problems are hard to come by -- maybe incentivize the problem writing a little bit more. If the budgets are a problem, then maybe introduce a tipping system where after the contest people may tip the writer for a good problem. A lot of us might want to reward good writers to keep the good problems keep coming.
I think it's more on the platform limitation that discourages people to write problems for TC.
Topcoder pays maybe best among all the platforms. But their software is bad :|
I was the setter for div1. 450 and 900
Consider a bipartite graph. Left side has one fake vertex and n vertices one for each shirt. Similarly, for right side. Connect source to a mid vertex with capacity k and cost 0. For each $$$i$$$, connect mid to shirt $$$i$$$ on left with capacity $$$1$$$ and cost -shirtValue[i]. Connect mid to fake shirt vertex with capacity infinity, cost 0. Repeat symmetrically on the right side. For each deal (i, j) connect shirt_i to jeans_j with capacity 1, cost 0. Connect shirt_i to fake jeans with capacity 1, cost 0. Connect fake shirt to jeans_j with capacity 1, cost 0. Finally, connect fake jeans and fake shirt with capacity infinity, cost 0.
Return negative of min cost max flow. Why does this work?
If for some deal both the shirt and jeans haven't been purchased already, route a unit flow from source -> mid -> shirt_i -> jeans_j -> sink. If the jeans has been purchased before but the shirt hasn't, route a path from source -> mid -> shirt_i -> fake jeans -> sink. If the shirt has been purchased before but the jeans hasn't, route a path from source -> mid -> fake shirt -> jeans_j -> sink. If both have been purchased before, route a path from source -> mid -> fake_shirt -> fake_jeans -> sink.
Note that we can actually get a faster solution by replacing negative edges (-x by MAX — x).
Sort A. Process in reverse. Maintain the probability that for all $$$j \geq i$$$, $$$a_j \leq A_i$$$. Lets call this probability $$$P_i$$$. Given this event, all $$$j \geq i$$$ are equivalent. Let $$$k = n - i$$$. There are two cases now:
All $$$j \geq i$$$ have $$$a_j \lt A_{i-1}$$$. In this case we go to the next step.
There are some $$$r \geq 1$$$ indices $$$j$$$ which have $$$a_j$$$ in range $$$[A_{i-1}, A_i]$$$. Here, the expected value should be $$$A_i - \frac{d}{r + 1}$$$. Let $$$d = A_i - A_{i-1}$$$, and $$$p = d / A_i$$$. We should add $$$P_i$$$ times $$$\displaystyle \sum_{r >= 1} \binom{k}{r} p^r (1-p)^{k-r} \left (A_{i} - \dfrac{d}{r+1} \right) = A_i - A_{i-1}(1-p) ^ k - \frac{d(1 - (1-p)^{k+1})}{p(k + 1)}$$$.
This can be proved using $$$\displaystyle \sum \binom{n}{i} \frac{q^{i + 1}}{i + 1} = \displaystyle \int_{0}^{q} (1 + x) ^ n dx = \dfrac{(1 + q) ^ {n + 1} - 1}{n + 1} $$$.
Note that the term to be added can be added without precision loss.
I asked the real value to avoid the solution which gets a formula from the integral formed for the expectation value, $$$ A_n - \displaystyle \sum_{i=0}^{n - 1} \dfrac{A_{i+1}^{n-i+1} - A_i^{n-i+1}}{S_{i+1} (n - i + 1)} $$$, where $$$S_i = \displaystyle \prod_{j>=i} A_j $$$. ( but it turns out even this solution can pass using careful computation.)
The 900 explanation is a bit too short for me... Can you elaborate on the part in which a sum turns into an integral?
I noticed this was necessary during the contest but didn't know how to do this, so at least to me it is not obvious. Reading the code makes it much clearer: if you have the probability $$$p_i$$$ that $$$j \geq i, a_j \le A_i$$$, to get $$$p_{i-1}$$$ you have to remove the cases in which $$$j \geq i, A_{i-1} \le a_j \le A_i$$$, so $$$p_{i-1} = p_i \left(1 - \left(\frac{A_i - A_{i+1}}{p}\right)^{n-i+1} \right)$$$.
Assume we had to find the sum over $$$r \geq 0$$$. We can erase the $$$r=0$$$ case later. Let $$$q = \frac{p}{1-p}$$$ $$$\displaystyle \sum_{r >= 0} \binom{k}{r} \left (A_{i} - \dfrac{d}{r+1} \right) p^r (1-p)^{k-r} $$$
= $$$ \displaystyle A_i - \displaystyle \sum_{r \geq 0} \binom{k}{r} (1-p)^k q^r \dfrac{d}{r + 1}$$$
= $$$\displaystyle A_i - \displaystyle \dfrac{d(1-p)^k}{q} \displaystyle \sum_{r \geq 0} \binom{k}{r} \dfrac{q^{r+1}}{r + 1}$$$
Note that the sum can be obtained from the integral $$$\displaystyle \int_{0}^{q} (1 + x) ^ k dx = \displaystyle \sum_{r\geq 0} \binom{k}{r} \displaystyle \int_{0}^{q} x^r dx = \displaystyle \sum_{r \geq 0} \binom{k}{r} \frac{q^{r + 1}}{r + 1}$$$
Solutions like the one you're trying to avoid can pass pretty easily: compute logarithms of summands, ignore those which are too small (they can't be too large) and add/subtract exponentials of the rest. Also, compute all logs as long doubles.
The Div1 900 — "seemed" very similar to TCO19 Round 3A 500, however, the difference of asking minimum/maximum made all the difference in some concepts of solutions (at least for me). Great.
My solution to div1. 450 failed system test.
When I submit the same code to the same problem in Practice Rooms, I got accepted (I tried multiple times).
How come?
Did you run the test too, just submitting in practice does not the test on it. You will need to go to practice options and run the tests.
He didn't.
Thx! I didn't know that. Now I can get FST in Practice Rooms.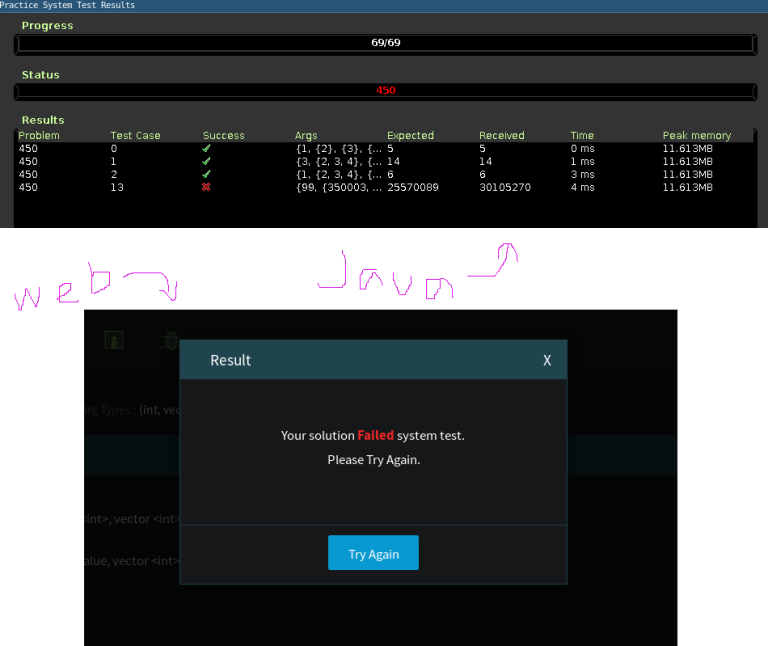
BTW, can I get full feedback in web arena like the one in java applet?
It just tells me that I failed.
How to do div2 900?
Because of the floating-point numbers, the Div. 1 900 was plagued with precision issues -- many of the competitors who failed would pass by replacing
doublewithlong double. Other competitors also managed to squeeze quadratic solutions through by quitting out early once the probabilities got low enough. I think the problem would have been better off asking for the expected value mod $$$10^9 + 7$$$.Yeah, I agree.
Actually, the intended solution is different than the accepted solutions, and there is no precision issue in the intended solution. Most of the solutions are making the formula that comes from breaking the obvious integral into n intervals pass. I couldn't think a way of calculating it precisely and was therefore under the impression that it can't be made to pass. Thinking that making the answer real would fail these solutions and the problem would actually be hard, I didn't use 10^9 + 7.
I think my solution is quite precise, by correctly joining each subtraction with addition (I mean, at least after you replace ii / (ii + 1) — (ii — 1) / ii with 1 / (ii * (ii + 1)), you only have additions)
My screencast with commentary: https://youtu.be/3oIrxt5Btvc
I respect that you are able to comment in English during the contest. Did you notice to be significantly slower because of that? Would speaking in Russian be easier for you? I'm just curious.
Just tried this today in the AGC, and it didn't seem to matter both objectively — still struggling to come up with correct algorithms — and subjectively — did not feel that different.
So I guess if I'm significantly slower, it does not depend on the language :)
For Div2 Easy, Hard (Also Div1 Easy) — prepared by me and mridul1809 and Div2 Medium — prepared by timmac
Now it's obvious that if $$$P > Q$$$, its impossible to make them equal.
When $$$P = Q$$$, we don't need to make any move.
Now when $$$P < Q$$$:
if $$$P + 1 = Q$$$, then its impossible to make them equal, no primes can be used.
else, to make maximum moves we will use only $$$2$$$'s and $$$3$$$'s! thus $$$(Q-P)/2$$$ will be the answer in that case.
We can generate all the rotations and flips of one of the grids and compare it with the other to get the answer with minimum number of defects.
Complexity: $$$O(n^2)$$$
An important observation: after performing the operations we will have elements left in at-most one of the three arrays. (If there are elements pending in more than 1 arrays, we can remove them and get a smaller remaining sum)
— The case where all the elements from all the arrays are cleared will be:
- Number of elements in any two arrays combined is atleast as much as the number of elements in the third array.
- Total number of elements is even.
If these two cases are satisfied simultaneously, then of course the first required value is 0 (no elements remaining), while the cost of removing them will be certain quantity $$$a*x + b*y + c*z + sum \ of \ all \ elements \ in \ all \ the \ arrays$$$— Now the case where its not possible to remove all the elements, some elements from an array will be left behind. Let's say, we leave $$$k$$$ elements from array $$$A$$$ (obviously the bigger $$$k$$$ elements to get minimum remaining sum). Now, we can check the new array $$$A'$$$, $$$B$$$ and $$$C$$$ for the case where no elements remain. If it is the case, then the answer will be (sum of elements left behind (sum of smaller $$$a-k$$$ elements from array $$$A$$$), cost found in clearing the remaining elements).
Therefore, we can get the best solution by iterating over $$$k$$$ on each of the arrays individually.
So it looks like one can pass Div2 Medium by trying the 3 rotations and one type of flip.
But there are four types of flip (vertical, horizontal, diagonal and antidiagonal) like this:
https://www.cs.umb.edu/~eb/d4/index.html
So, it may be nice in the problem statement to describe the "flip" more precisely. I first tried to implement all the four types of flips and then spent a lot of time thinking about whether the order of operations matters (reading the above web page, etc.), but the intended solution was much simpler. (Luckily I was not in the contest, just practice).
Nice problem otherwise, great for division 2 500. Thanks!
Hey royappa !
You can perform rotations and flips together as well! So a flip along diagonal is same as horizontal flip along with a rotation!
Total number of ways of arranging them will be 8 (4 x 2) ( 4 rotations , 2 flips ).
So the different flips you mentioned are actually being covered in the testcases.
I would suggest you that you should go over you code once again as your logic seems right!
coud you give some intuition on why using only 2s and 3s is sufficient
You need to maximize the number of moves. So you need to move using small primes. Since 2 covers only even difference between $$$P$$$ and $$$Q$$$, we also use 3 for odd differences.
I see, thanks.
Hi, In Div2 Hard, how will the cost of removing be a∗x+b∗y+c∗z+sum of all elements in all the arrays. I understand the sum of all elements part, but I have having trouble understanding a∗x+b∗y+c∗z. Could you please explain why that would be true ?
Bonus : Solve div1 450 for a general graph :
Given a graph with weights on vertices, find the maximum weight of a subset of vertices that can be covered by $$$k$$$ edges of the graph.
It is obviously not easier than matching in general graph, and reduction to weighted matching in general graph is easy. Doesn't look like a good problem.
I don't think I have an easy reduction. How do you reduce it?
For each vertex $$$v$$$ with non-zero degree let's add dummy vertex connected only to $$$v$$$ with weight 0. Now we can always choose $$$k$$$ edges such that they are a matching.
I am so tired of writing code to generate large arrays in topcoder. I know their system doesn't allow large inputs but it's still pretty bad.
This one felt especially bad since the B array was generated differently from the other for whatever reason, so you needed to be careful with the copy paste :.
Maybe they should have only one way of generating random arrays (probably the one that the first 1000 elements are given and you generate the rest, so it's easier to hack), and then just have sample code in all the languages.
But for Div1 300 this time, if testcase is not random (like first 500 elements are given), it will be very tricky. Even success rate 25.0% is possible. That's because:
I don't quite get the issue. The method they usually do, like they did for 900, let's you generate random tests like A but also manual ones, so you just have more options.
Also more importantly I am tired of writing the code to generate large arrays. They should either update the platform or make a easier way to generate the large arrays.
I also remember when the problems had small N, but using the same idea you could solve it will large N, but since the idea was the hard part, they could just keep N small.