Articulation Points
Let's define what an articulation point is. We say that a vertex $$$V$$$ in a graph $$$G$$$ with $$$C$$$ connected components is an articulation point if its removal increases the number of connected components of $$$G$$$. In other words, let $$$C'$$$ be the number of connected components after removing vertex $$$V$$$, if $$$C' > C$$$ then $$$V$$$ is an articulation point.
How to find articulation points?
Naive approach O(V * (V + E))
For every vertex V in the graph G do
Remove V from G
if the number of connected components increases then V is an articulation point
Add V back to G
Tarjan's approach O(V + E)
First, we need to know that an ancestor of some node $$$V$$$ is a node $$$A$$$ that was discoverd before $$$V$$$ in a DFS traversal.
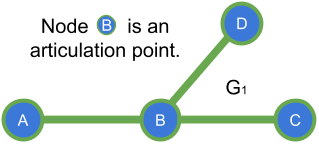
In the graph $$$G_1$$$ shown above, if we start our DFS from A and follow the path to C through B ( A -> B -> C ), then A is an ancestor of B and C in this spanning tree generated from the DFS traversal.
Example of DFS spanning trees of a graph
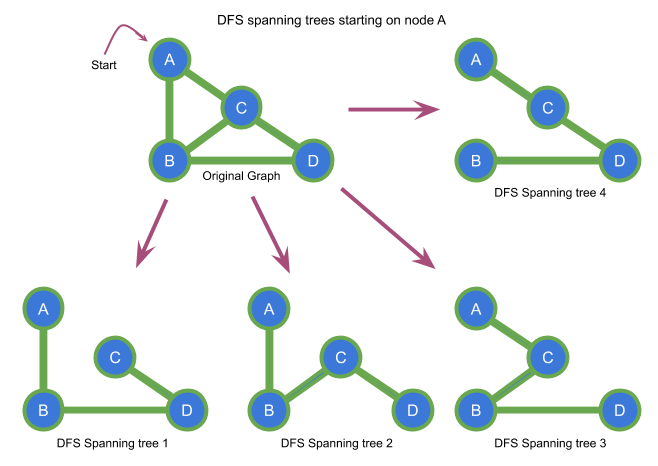
Now that we know the definition of ancestor let's dive into the main idea.
Idea
Let's say there is a node $$$V$$$ in some graph $$$G$$$ that can be reached by a node $$$U$$$ through some intermediate nodes (maybe non intermediate nodes) following some DFS traversal, if $$$V$$$ can also be reached by $$$A$$$ = "ancestor of $$$U$$$" without passing through $$$U$$$ then, $$$U$$$ is NOT an articulation point because it means that if we remove $$$U$$$ from $$$G$$$ we can still reach $$$V$$$ from $$$A$$$, hence, the number of connected components will remain the same.
So, we can conclude that the only 2 conditions for $$$U$$$ to be an articulation point are:
If all paths from $$$A$$$ to $$$V$$$ require $$$U$$$ to be in the graph.
If $$$U$$$ is the root of the DFS traversal with at least 2 children subgraphs disconnected from each other.
Then we can break condition #1 into 2 subconditions:
- $$$U$$$ is an articulation point if it does not have an adyacent node $$$V$$$ that can reach $$$A$$$ without requiring $$$U$$$ to be in $$$G$$$.

- $$$U$$$ is an articulation point if it is the root of some cycle in the DFS traversal.
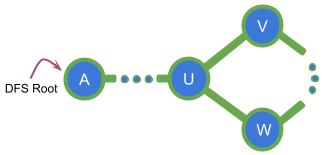
Examples:

Here B is an articulation point because all paths from ancestors of B to C require B to be in the graph.

Here B is NOT an articulation point because there is at least one path from an ancestor of B to C which does not require B.
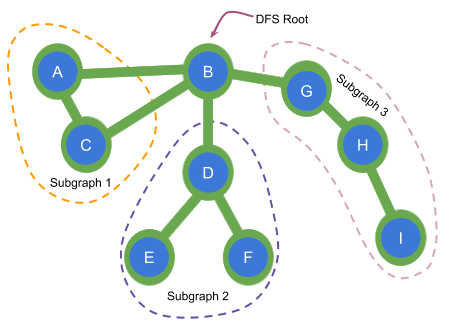
Here B is an articulation point since it has at least 2 children subgraphs disconnected from each other.
Implementation
Well, first thing we need is a way to know if some node $$$A$$$ is ancestor of some other node $$$V$$$, for this we can assign a discovery time to each vertex $$$V$$$ in the graph $$$G$$$ based on the DFS traversal, so that we can know which node was discovered before or after another. e.g. in $$$G_1$$$ with the traversal A -> B -> C the dicovery times for each node will be respectively 1, 2, 3; with this we know that A was discovered before C since discovery_time[A] < discovery_time[C].
Now we need to know if some vertex $$$U$$$ is an articulation point. So, for that we will check the following conditions:
If there is NO way to get to a node $$$V$$$ with strictly smaller discovery time than the discovery time of $$$U$$$ following the DFS traversal, then $$$U$$$ is an articulation point. (it has to be strictly because if it is equal it means that $$$U$$$ is the root of a cycle in the DFS traversal which means that $$$U$$$ is still an articulation point).
If $$$U$$$ is the root of the DFS tree and it has at least 2 children subgraphs disconnected from each other, then $$$U$$$ is an articulation point.
So, for implementation details, we will think of it as if for every node $$$U$$$ we have to find the node $$$V$$$ with the least discovery time that can be reached from $$$U$$$ following some DFS traversal path which does not require to pass through any already visited nodes, and let's call this node $$$low$$$.
Then, we can know that $$$U$$$ is an articulation point if the following condition is satisfied: discovery_time[U] <= low[V] ( $$$V$$$ in this case represents an adjacent node of $$$U$$$ ). To implement this, in each node $$$V$$$ we will store some identifier of its corresponding node $$$low$$$ found, this identifier will be the corresponding $$$low's$$$ discovery time because it helps us to know when the node $$$low$$$ was discovered, hence it helps us to know by which node we can discover $$$U$$$ first.
C++ Code
// adj[u] = adjacent nodes of u
// ap = AP = articulation points
// p = parent
// disc[u] = discovery time of u
// low[u] = 'low' node of u
int dfsAP(int u, int p) {
int children = 0;
low[u] = disc[u] = ++Time;
for (int& v : adj[u]) {
if (v == p) continue; // we don't want to go back through the same path.
// if we go back is because we found another way back
if (!disc[v]) { // if V has not been discovered before
children++;
dfsAP(v, u); // recursive DFS call
if (disc[u] <= low[v]) // condition #1
ap[u] = 1;
low[u] = min(low[u], low[v]); // low[v] might be an ancestor of u
} else // if v was already discovered means that we found an ancestor
low[u] = min(low[u], disc[v]); // finds the ancestor with the least discovery time
}
return children;
}
void AP() {
ap = low = disc = vector<int>(adj.size());
Time = 0;
for (int u = 0; u < adj.size(); u++)
if (!disc[u])
ap[u] = dfsAP(u, u) > 1; // condition #2
}
Bridges
Let's define what a bridge is. We say that an edge $$$UV$$$ in a graph $$$G$$$ with $$$C$$$ connected components is a bridge if its removal increases the number of connected components of $$$G$$$. In other words, let $$$C'$$$ be number of connected components after removing edge $$$UV$$$, if $$$C' > C$$$ then the edge $$$UV$$$ is a bridge.
The idea for the implementation is exactly the same as for articulation points except for one thing, to say that the edge $$$UV$$$ is a bridge, the condition to satisfy is: discovery_time[U] < low[V] instead of discovery_time[U] <= low[V]. Notice that the only change was comparing strictly lesser instead of lesser of equal.
But why is this ?
If discovery_time[U] is equal to low[V] it means that there is a path from $$$V$$$ that goes back to $$$U$$$ ( $$$V$$$ in this case represents an adjacent node of $$$U$$$ ), or in other words we can just say that we found a cycle rooted in $$$U$$$. For articulation points if we remove $$$U$$$ from the graph it will increase the number of connected components, but in the case of bridges if we remove the edge $$$UV$$$ the number of connected components will remain the same. For bridges we need to be sure that the edge $$$UV$$$ is not involved in any cycle. A way to be sure of this is just to check that low[V] is strictly greater than discovery_time[U].
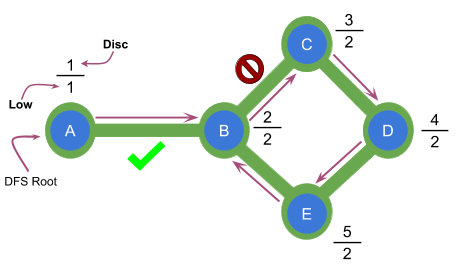
In the graph shown above the edge $$$AB$$$ is a bridge because low[B] is strictly greater than disc[A]. The edge $$$BC$$$ is not a bridge because low[C] is equal to disc[B].
C++ Code
// br = bridges, p = parent
vector<pair<int, int>> br;
int dfsBR(int u, int p) {
low[u] = disc[u] = ++Time;
for (int& v : adj[u]) {
if (v == p) continue; // we don't want to go back through the same path.
// if we go back is because we found another way back
if (!disc[v]) { // if V has not been discovered before
dfsBR(v, u); // recursive DFS call
if (disc[u] < low[v]) // condition to find a bridge
br.push_back({u, v});
low[u] = min(low[u], low[v]); // low[v] might be an ancestor of u
} else // if v was already discovered means that we found an ancestor
low[u] = min(low[u], disc[v]); // finds the ancestor with the least discovery time
}
}
void BR() {
low = disc = vector<int>(adj.size());
Time = 0;
for (int u = 0; u < adj.size(); u++)
if (!disc[u])
dfsBR(u, u)
}
FAQ
- Why
low[u] = min(low[u], disc[v])instead oflow[u] = min(low[u], low[v])?
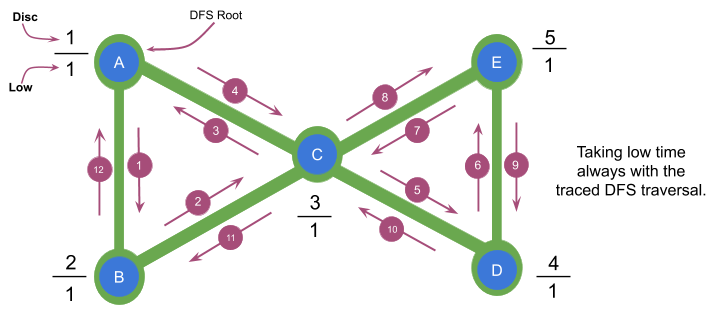
Let's consider node C in the graph above, in the DFS traversal the nodes after C are: D and E, when the DFS traversal reaches E we find C again, if we take its $$$low$$$ time, low[E] will be equal to disc[A] but at this point, when we return back to C in the DFS we will be omitting the fact that $$$U$$$ is the root of a cycle (which makes it an articulation point) and we will be saying that there is a path from E to some ancestor of C (in this case A) which does not require C and such path does not exist in the graph, therefore the algorithm will say that C is NOT an articulation point which is totally false since the only way to reach D and E is passing through C.











$$$+\text{TREE}(\text{G}(64))$$$ $$$\text{prro :v}$$$ $$$\square$$$
The best explanation that I found, i've been looking for someone who could explain this subject, and I think I found that guy. +10 and to favorite.
can you also explain how to find the biconnected components?
Good tutorial with nice explanations and examples
I think there is a little mistake
one doubt, help please can i get all the edges which are part of a cycle by changing the condition in bridge code ??
You can create an array containing the parents of each of the nodes in the path, however you might be looking for Strongly Connected Components which uses a very similar idea. I recommend you to read about that topic. Now that you understood Tarjan's Idea it will be very straight forward for you to understand Strongly Connected Components
yes,i know about that but i guess it's complexity is (exponential) very bad. That is why i am looking for an aternate .Thank you btw
How did you make these drawings?
They look great.
Can we use " low[u] = min(low[u], low[v]) " while finding bridges, I am not able to draw a case where it will not work while finding bridges? Thanks
I am not able to draw case either. Which makes sense to me since the condition to find a bridge is
disc[u] < low[v]and noticing the strict lesser condition, we can observe that in the case of bridges we don't care about the node that is the root of a cycle, which was the case that we should consider for Articulation Points. In conclusion by the informal proof, when finding just bridges you could uselow[u] = min(low[u], low[v]), I suggest you to make a more formal proof of this just to be sure.Thanks
Good explanation ;_;
Does anybody have links to problems based on above approach??
It would be very helpful.
Thanks in advance.
I just added a "problems" section in the post :D
In case where we found an ancestor of the node, why do we minimise the low time of the node with discovery time of ancestor and not low time of ancestor.
I mean why not
Because if you use the lowest of that ancestor, it can point way too high
https://pasteboard.co/JTasj2Y.jpg
in this example if node 5 uses the lowest in node 3 in which theres a back edge to the root, node 3 will not be detected as an ap because its lowest in its subtree is 1 even though it should just be 3.
Interesting. Thank you very much for this counter example. I appreciate!
image not found
@xdlolhahatt can you reshare the image. Its coming as NOT FOUND
Question about articulation points.
From the code, it seems like failing condition #2 would overwrite condition #1?
So what if ap[u] = 1 because this is true:
if (disc[u] <= low[v]) // condition #1 ap[u] = 1;But then when you exit out of the dfs, could this be set to 0 because let's say the dfs only returned 1 children?
I assume that condition 1 could be true when condition 2 isn't (otherwise we would just check for condition 2), so wouldn't this be an issue?
ap[u] = dfsAP(u,u)>1 ; this condition is only applied on the roots of the components so we don't care if it overwrites condition #1. Cuz anyway for roots we are checking only condition #2.
The explanation was so good. This guy deserves more upvotes.
whats wrong in my code i have used the same logic for articulate point.
Please someone help me, I have given 2-3 days i want to know what I have been doing wrong.
Here is a response from GPT-4, perhaps it can be helpful (I'm too lazy to read your code): It appears that you are trying to implement Tarjan's algorithm to find articulation points in a given graph. Let's analyze the code and point out possible issues:
Parent Check: It seems like the algorithm is trying to check whether an adjacent node is the parent of the current node. But the check
adj[x][i] != parent and adj[x][i] != xcould lead to skipping necessary nodes if the graph contains self-loops or multiple edges. The logic of the DFS traversal should be able to handle self-loops and multiple edges without requiring specific checks.Handling Disconnected Graph: The code makes a single call to
dfs(low, depth, v, -1, 0, ans, adj)and then tochk(1, adj, v), assuming that the graph is connected. If the graph is not connected, some vertices may not be visited by these calls, leading to an incorrect result. You may need to implement logic to handle multiple connected components.Initialization of 'low' and 'depth': The code initializes both
lowanddepthto 0 for all vertices. While initializingdepthto 0 is correct, the initialization oflowshould be done inside the DFS function, where it should be initialized to thedepthof the current node. This ensures that thelowvalue is correctly computed for every node.Implementation Complexity: The code can be simplified by removing the separate
chkfunction and integrating its functionality into the main DFS function. The special handling for the root (withelif x == 0:) is also unnecessary and adds complexity.Here is a revised version of the code:
The changes address the identified issues and simplify the code, preserving the algorithm's functionality to find articulation points.
.
Raj_Raghu
Great explanation. Thank you so much.