VietCT's blog

Help with segment in a tree problem
By VietCT, history, 5 years ago, In English

Hi guys.

I have a problem want to ask you guys.

Problem: Given a tree with n nodes, m segments in a tree with 2 endpoints. Find the maximum number of segments satisfy that not exist two segments with the edge intersect. (n < 1e3, m < 1e5);

My solution (WA passed 4/5) is: Sort m segments by the depth of their LCA. If two segments have the same LCA, if one of them have the endpoint equal to their LCA i choose it ,else i choose the one have shorter length. After sorted, i pick it one by one.

My sub For example:

n = 6, m = 4;

edges:

1 2

2 3

3 4

3 5

3 6

segments:

1 3

4 5

5 6

6 4

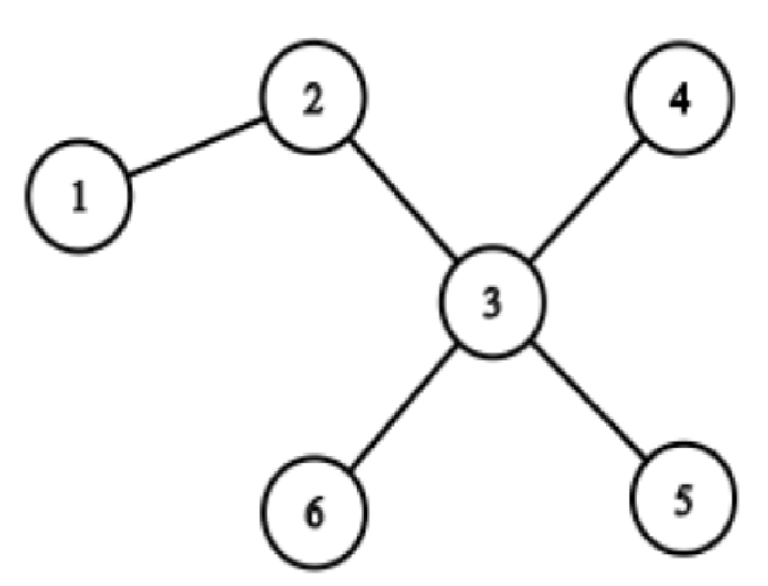
So the answer is 2 because we can choose segment (1, 3) and segment (4, 5) as path 1 -> 3 = 1 -> 2 -> 3, path 4 — > 5 = 4 — > 3 -> 5.

You also can choose (1, 3), (5, 6) or (1, 3), (6, 4)

  • Vote: I like it
  • 0
  • Vote: I do not like it

Comments Comments (9)
| Write comment?
»
5 years ago, # |
  Vote: I like it -7 Vote: I do not like it

Can you give link or something? Or at least explain better. Please don't expect people to understand what you mean by "Find the maximum number of segments satisfy that not exist two segments with the paths intersect."

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Sorry for my bad english i will add an example to make it more clear

    → Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    It is clear enough bro?

    → Reply
    • »
      »
      »
      5 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Ok, now I understand. Do you have any proof/intuition why your greedy algorithm should always produce the optimal solution? To me it is not at all clear why it should work — seems like unproven greedy.

      → Reply
      • »
        »
        »
        »
        5 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        My greedy algorithm is completely wrong. You have any ideas?

        → Reply
        • »
          »
          »
          »
          »
          5 years ago, # ^ |
            Vote: I like it +1 Vote: I do not like it

          How about something like: let $$$\mathrm{dp}[u]$$$ be the most segments that can be fit completely in the subtree of $$$u$$$.

          → Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

you miss one important detail that degree of each node is less than 10

→ Reply