Предлагаю обсуждать здесь задачи.
Как решать H? Правда ли, что при детерминизации недетерминированного автомата, построенного естественным образом по дереву, состояний получится не очень много?
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Предлагаю обсуждать здесь задачи.
Как решать H? Правда ли, что при детерминизации недетерминированного автомата, построенного естественным образом по дереву, состояний получится не очень много?
| Название |
|---|



sankear сейчас напишет, как мы упихали H. А как решать C?
Идем построчно, и для каждой строки по очереди добавляем столбцы, начиная со столбцов с наибольшей высотой (т.е. с наибольшим количество подряд идущих нулей, которые заканчиваются в текущей строке). И поддерживаем для каждого куска сколько у него есть слева (т.е. в префиксе) уже добавленных столбцов, сколько справа (т.е. в суффиксе) и сколько кусков добавлены полностью. Для того чтобы после очередной добавленной высоты найти максимальную ширину, мы можем взять два куска с максимальной левой шириной и два куска с максимальной правой шириной (по два надо в том случаи если с максимальной левой шириной кусок это и есть кусок с максимальной правой шириной, т.е. мы используем один и тот же кусок дважды) и учесть куски, которые добавлены уже целиком.
Сложность выходит O(SlogS), где S максимальная площадь карты, т.е. ≤ 105.
У нас очень простое решение, за O(WH·min(W, H)) = O((WH)1.5). Пойдём по строкам, будем поддерживать для каждого столбца каждого куска текущую высоту столбца из нулей. Как найти максимальную площадь для прямоугольника, оканчивающегося на данной высоте? Переберём высоту прямоугольника (кандидатов min(W, H), т.к. имеет смысл перебирать только высоты, являющиеся текущими высотами какого-то из столбцов), для каждой высоты итерируемся по всем кускам и считаем ответ (крайние куски добавляют немного геморроя).
Не знаю как кто, но мы сдали что-то странное =) Построим бор по запросам, для каждой вершины посчитаем минимальную глубину, на которой есть вершина с запросом. Теперь будем в рандомном порядке подвешивать дерево, при обходе дерева обходим и бор, как только нашли вершину с запросами, то ответили на них. Не идем по дереву, если нет перехода по бору. Если в какой-то момент в поддереве вершины бора не осталось запросов, удаляем эту вершину. Ну и еще отсекаемся по длине максимального возможного пути в дереве. Это получает ТЛ 93, если еще добавить отсечение по времени, то это заходит. Интересно узнать честное решение =)
Не понятно, за что минусуют: вроде решение норм.
Нельзя сказать что очень честное, но работает без отсечения по времени, оценивать асимптотику не умеем, а еще есть подозрение, что просто макс.тест настолько специфический, что его заранее построить невозможно. А решение такое:
Посчитаем хеши всех префиксов и всех перевернутых суффиксов запросов, для каждой полученной пары <хеш, длина подстроки> сделаем set того, чем она является (префикс или суффикс и в каком запросе). Далее динамика по дереву — для каждой вершины храним set pair<хеш,длина> всевозможных путей из этой вершины, мержим два сета за O(размер меньшего set'а) (для этого надо хранить пару не в явном виде а как линейную функцию от нее и при добавлении вершины пересчитывать коэффициенты), при этом для каждого хэша из меньшего множества проверяем частью какой строки он может являться (при помощи тех самых заранее построенных сетов) и обновляем ответы, как только мы нашли одно вхождение строки, сразу удаляем из сетов, при этом если хеш уже не может быть частью ни одной строки, то про него надо забыть, т.к. потом и подавно мы с его помощью ничего не найдем.
Как вы проходите такого вида тесты:
на всех ребрах, допустим, написана буква a, и все запросы состоят из букв a.
Меньшее множество будет состоять из одной строки "a", но придется проверять все запросы, т.к. они все начинаются на 'a'. И так на каждом шаге. O(n) раз. Weak tests или мы что-то упустили?
В задаче были числа, а не буквы, но я думаю, меня поняли.
После первого же сливания мы ответим на все запросы и выкинем их из сетов, сделав их пустыми и дальше мы будем уже просто сливать сеты для вершин, т.к. теперь для любого хеша просто нет необработанных запросов, легко доказывается, что это работает за O(n*((logn)^2)).
Ну а если ни один запрос не подошел и никогда не подойдет? Но все, что в текущий момент в сете, является префиксом какого-либо запроса? Тогда придется таскать до самого корня много-много хешей. И при каждом мерже все их придется проверять.
Да, согласен, если бы все запросы были "ab", а не просто "a", то да, получился бы (n^2)*logn. Ну, значит тесты очень клевые)
Жалко, мы придумали именно это решение, но после того как нашли такой тест и некоторые другие, решили написать gg и выйти
Предполагалось такое решение:
(a) Предположим, что у нас в строках запросов соседнии символы не равны: si ≠ si + 1, в конце, будет пояснено, как избежать этого ограничения.
1) Допустим у нас всего одна строка s в запросе. То можно решать разными способами, но один из них может быть таким: Предположим, что строка проходит через вершину u, проверим, что это так: например, собрав хэши по путям из вершины u, наша строка проходящая через u будет состоять из двух путей: пути из u — являющимся перевернутым префиксом строки s и пути из u являющимся суффиксом строки s. Предположение (a) гарантирует, что они не попадут в одно поддерево. В таком случае можно для каждого пути из этого дерева искать соответствующий перевернутый префикс (можно хэшами) и смотреть, есть ли в этом дереве хэш соответствующего суффикса. Если это не так (т.е. строка не проходит, через u), то выкинем вершину u, дерево распадется на несколько меньших деревьев и для каждого нового дерева, запустим эту процедуру повторно. Если в качестве u каждый раз выбирать "центр" графа — вершину у которой максимальное из поддеревьев ≤ размер поддерева / 2, то глубина такой операции будет O(log(n)), а суммарное количество вершин в деревьях на всех этапах (и путей для которых считаются хэши) -- O(nlog(n)). Но если на входе много запросов, то решить так не сможем.
2) Промоделируем процесс из п.1, т.е. каждый раз будем искать центр графа, выкидывать его, и повторять для каждого из новых деревьев. И сохраним все эти деревья Ti. Для каждого такого дерева посчитаем хэши путей и составим из них множество Si. Таких множеств O(n) и суммарное количество элементов в них, как было написано в п.1, O(nlog(n)). Теперь для каждой строки, рассмотрим каждое из ее разбиений на пару префикс + суффикс, тогда нам нужно уметь быстро определять, есть ли такое множество Si в котором есть и перевернутый префикс и суффикс, но проблема в том, что множества Si между собой пересекаются. Для этого можно применить следующий прием: составим граф из вершин -- все различные префиксы и суффиксы строк их O(m), где m будет суммарной длиной всех строк-запросов, а ребро между двумя вершинами u и v, если есть строка u + v. Будем теперь проходиться по каждому из множеств Si и красить все вершины, которые входят в Si в цвет i, тогда если мы будем знать набор ребер, которые в какой момент времени были покрашены в один цвет (т.е. это будет означать, что и u и v лежат в одном дереве), то сможем ответить, какие строки входят в дерево, ну и если красить с дополнительной информацией (т.е. еще сохранять путь в исходном дереве, который соответствует данной вершине), то можно восстановить и само вхождение.
3) Как сделать п.2 эффективно: можно применить стандартный прием, который вроде бы называется корневой эвристикой: разобьем все вершины в графе префиксов и суффиксов на два множества: те у кого инцидентных ребер больше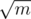 -- назовем их большими, и у тех у кого не больше -- назовем их маленькими. Теперь когда рассматриваем какое-то дерево Si -- просто покрасим все вершины соответствующие какому-то хэшу из Si в цвет i. Теперь пройдемся по тем вершинам которые красили в цвет i, пусть мы сейчас рассматриваем некоторую вершину u этого графа, то если u является маленькой, то можно влоб пройтись по всем инцидентным ребрам этой вершины и проверить является ли ребро "одноцветным", если является, то как-нибудь его пометить. Это позволит рассмотреть ребра с двумя маленькими вершинами и одной маленькой и одной большой вершинами. Если вершина u большая, то пройдемся по инцидентным ей большим вершинам (их не больше
-- назовем их большими, и у тех у кого не больше -- назовем их маленькими. Теперь когда рассматриваем какое-то дерево Si -- просто покрасим все вершины соответствующие какому-то хэшу из Si в цвет i. Теперь пройдемся по тем вершинам которые красили в цвет i, пусть мы сейчас рассматриваем некоторую вершину u этого графа, то если u является маленькой, то можно влоб пройтись по всем инцидентным ребрам этой вершины и проверить является ли ребро "одноцветным", если является, то как-нибудь его пометить. Это позволит рассмотреть ребра с двумя маленькими вершинами и одной маленькой и одной большой вершинами. Если вершина u большая, то пройдемся по инцидентным ей большим вершинам (их не больше 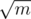 ) и проверим — являются ли они одного цвета, если являются, то пометим эти ребра. Это рассмотрит случай ребра с двумя большими вершинами.
) и проверим — являются ли они одного цвета, если являются, то пометим эти ребра. Это рассмотрит случай ребра с двумя большими вершинами. 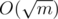 операций. А операций покраски O(nlog(n)), т.е. суммарное время
операций. А операций покраски O(nlog(n)), т.е. суммарное время 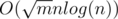 . Когда есть список таких помеченных ребер, то можно просто для каждой строки из запросов проверять, помечена ли какая-нибудь из пар префикс + суффикс.
. Когда есть список таких помеченных ребер, то можно просто для каждой строки из запросов проверять, помечена ли какая-нибудь из пар префикс + суффикс.
После прохода по всем множествам Si у нас есть список помеченных ребер, которые были покрашены в какой-то момент в один цвет (т.е. есть какое-то Si которому принадлежат обе вершины).
Понятно, что на каждую из вершин потратится
Дополнения:
* Как можно избавиться от предположения (a): Для этого вершины можно красить не в цвет i, когда мы рассматриваем множество Si, а в (i, v), где v будет корнем поддерева Ti в котором лежит соответствующий путь и в каждой вершины сохранять по две различных расскраси. Тогда нужно будет проверять, не то что цвета равны, а то что найдется из цветов, такие пары, что первые элементы цветов равны, а вторые не равны (т.е. лежат в одном дереве, но в разных поддеревьях).
** Можно построить решение без хэшей с той же ассимптотикой, для этого изначально необходимо построить суффиксное дерево на строках si, rev(si), где rev(a) — это перевернутая строка. Строить его надо — разделив все соотвествующими разделителями, т.е. для строки вида s1#1rev(s1)#2s2#3rev(s2)... sn#2n - 1rev(sn)#2n. Тогда вместо хэша можно рассматривать состояние в суффиксном дереве. Для перевернутого префикса и не перевернутого суффикса — эти состояния получить легко. Теперь необходимо так же занумеровать пути из деревьев Ti, для этого можно просто обходить эти деревья и параллельно идти по суффиксному дереву и сохранять в виде хэша -- состояние в суффиксном дереве. Нужно учитывать, что если по какому-то символу из u нет перехода из текущего состояния, то переходить в дереве Ti из u по этому символу нельзя -- таких префиксов и суффиксов все равно нет.
*** в п.2. можно не сохранять все деревья Ti, а использовать линейное количество памяти: проверить по п.3. текущее дерево, удалить оттуда корень и запустить соответствующую процедуру рекурсивно.
Если интересуют какие-то отдельные детали — буду рад пояснить. К сожалению, тесты не смогли покрыть все эвристики по этой задаче, но надеюсь она все равно хоть кому-нибудь понравилась =).
Интересно, это фича, что в Е заходит абсолютно тупой кун?
Какое нормальное решение?
Без жадности?! Мы честно пытались валить его с жадностью, когда cmd придумал решение за O(N), но так ничего и не вышло...
Без жадности. Пришлось правда часть векторов заменить на массивы.
По-моему, то, что там заходит абсолютно тупой Кун, было очевидно, начиная с момента времени 2:26.
Кстати, одно из АС-решений по Е с использованием "тупого" Куна в дорешивании стабильно получает ТЛ 21. Для дорешивания используются другие серверы?
Я в дорешку и сдавал. Попробуй пооптимизить
А что такое Кун с жадностью? Паросочетание-то стоимостное, жадно инициализировать нельзя.
Наверное жадность не совсем точно сказано, имелось ввиду при поиске пары для вершины сперва проверить есть ли свободные, а если нет свободных, то пробовать уже освободить кого-нибудь. При обработке это будет немножко похоже на жадность по-моему.
там веса только в одной доле графа, в этом случае можно а как решать без жадности?
Нормальное решение такое. Построим двудольный граф с весами, взятыми из матрицы. Задача свелась к такой: надо для каких-то вершин выбрать рёбра, так что для каждой вершины выбрано <=одно ребро, для каждого ребра <=1 вершина, и сумма весов рёбер максимальна. Несложно заметить, что допустимые подмножества — это наборы компонент связности, где каждая компонента — дерево + (возможно) одно ребро. Утверждается, что такие штуки можно искать жадно, аналогично алгоритму Краскала.
Как можно строить граф: слева у нас будет N * M вершин (вершины соответствует клеткам), справа будет N + M вершин (для строк и столбцов). Клетка соединяется со строкой и со столбцом в которой находится. Вес в данном случаи имееют только вершины в левой доли (клетки). Если не нужно восстанавливать паросочетание, а только найти его оптимальный вес, то можно это сделать за O(N) используя DSU, учитывая что для каждой вершины левой доли есть только 2 ребра в правую.
Как решать F?
Если втупую (за квадрат) — для каждой вершины dfs'ом считаем вероятность того, что она плохая, потом по линейности матожидания суммируем эти вероятности. Теперь оптимизация — когда вызываемся dfs'ом из вершины x, придя в неё из вершины y, запоминаем ответ для пары (x, y) (т.е. грубо говоря, для ориентированного ребра). Это уже работает за линию.
Подробнее: сначала решим задачу для какого-то одного пассажира. Подвесим за него дерево и посчитаем такую динамику: d(root) — вероятность того, что в поддереве с корнем root собственно корень выйдет из автобуса и не вернётся (т.е. если зафиксировать распределение на спящих, неспящих и вышедших, то не найдётся пути из корня в неспящего, который не прошёл бы через спящего. В таком случае некому будет позвонить корню). Что для этого нужно? Для этого каждый из его детей должен или спать, или выйти из автобуса и не вернуться. Кроме того, сам корень должен выйти из автобуса: . Подвесив дерево за каждого пассажира, мы получим решение за O(N2), так как ответ из-за линейности мат. ожидания — это сумма всех d(root).
. Подвесив дерево за каждого пассажира, мы получим решение за O(N2), так как ответ из-за линейности мат. ожидания — это сумма всех d(root).
Теперь можно, например, создать фиктивную вершину, пустить из неё односторонние рёбра во все остальные и один раз посчитать эту динамику для неё. Или, что то же самое, сделать параметром динамики не просто корень, а ориентированное ребро: корень и его предок. Такое решение работает уже за линию.
UPD. Или нет. Но довести до линии всё равно можно: один раз подвесим дерево и посчитаем d(v) для всех вершин. Теперь значение в корне именно то, которое нам нужно, а в его сыновьях немного другое: каждый сын знает ответ в предположении, что дерево подвешено за него, но родителя не существует. Это можно исправить так: перед тем как идти по ребру (parent, child) в поиске в глубину, надо домножить значение d(child) на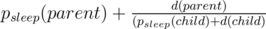 . Это как раз недостающий член в произведении. Деление возникает чтобы учесть тот факт, что child после переподвешивания уже не будет ребёнком parent.
. Это как раз недостающий член в произведении. Деление возникает чтобы учесть тот факт, что child после переподвешивания уже не будет ребёнком parent.
UPD2. Это почти то же самое, что написано два раза ниже в треде :О) Код: http://pastie.org/7689104
А поясните, пожалуйста, если не сложно, как такая динамика работает за линию на "звезде" (в которой (N-1) листьев)?
О, это очень хороший вопрос, спасибо. Никак. Зато если вы не помните, что это стандартный способ её свалить, то можно пропихнуть задачу =/
Хотя, возможно, ilyakor что-то другое имел в виду
Хехе... Никак она не работает, точнее, за квадрат. Об этом я не подумал :( Состояний там конечно линия, но не переходов. Соптимизить вроде можно, но мы этого не делали. Т.е. у жюри такого теста почему-то не было.
Я, может, слегка повторю вышенаписанное, во всяком случае одну формулу выше — точно. Но у меня честное простое решение за линию.
Опять же, решаем для одного пассажира, который, для определённости, корень дерева. Понятно, что он должен оказаться в компоненте из ушедших людей, причём ограниченной со всех сторон спящими людьми. Пишем соотношение выше: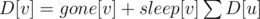 по всем детям u вершины v — это вероятность того, что в поддереве вершины v наблюдается картина, описанная в предыдущем предложении. Тогда ответ для корня это D[root] - sleep[root].
по всем детям u вершины v — это вероятность того, что в поддереве вершины v наблюдается картина, описанная в предыдущем предложении. Тогда ответ для корня это D[root] - sleep[root].
Теперь, давайте раскроем все скобочки в этой динамике. Получится штука следующего вида — ответ для корня это сумма вообще по всем вершинам v произведения sleep[v]·gone[v1]·gone[v2]·..., где v1, v2, v3, ... — путь до корня от вершины v.
Теперь относительно ясно, как за один DFS посчитать такую хрень по всем корням в сумме. Нужно просто в DFS передавать ещё одним параметром накопленную часть суммы по наддереву — тогда переходя по ребру вниз просто добавим туда всё, что придёт из остальных поддреревьев текущей вершины. То есть стандартный способ обобщения динамики по поддереву на динамику в том числе и по наддереву.
Вот код: http://pastie.org/7685000
Магия во втором DFS'e призвана полечить проблему с делением нуля на ноль (когда вероятности становятся меньше 1e-300, дабл зануляется и происходит дребедень, приходится использовать только умножением, для чего я насчитываю произведения на префиксах и на суффиксах, а потом их использую в переходе по ребру).
Макс, это то же, что и у нас, и уже с успехом обсудили где-то внизу. А код ОК: покороче, чем у Игоря. :)
Мы в этом коде проверяли элемент на 0 с эпсилоном. Если не ноль — делим, если ноль — ставим флажок, что остальные нули, а произведением считаем фором.
Подвешиваем дерево за любую вершину. Первым обходом для каждой вершины узнаем вероятность того, что для поддерева с текущей вершиной она вышла из автобуса (т.е. она вышла и её никто обратно в автобус не позвал), т.е. это вероятность того, что текущая вершина вышла и все её сыновья вышли или спят. А потом вторым обходом будет пропихивать вероятность того, что предок спит или вышел (обратно имеется ввиду, что вершина вышла и её не позвали обратно в автобус), тогда в мы знаем для текущей вершины вероятнсть того, что её никто не позовет снизу в поддереве и вероятность того, что предок тоже её звать не будет... надо только научиться пропихивать вероятность сверху.
На мой взгляд, там самое сложное оказалось правильно обрабатывать нулевые вероятности. По крайней мере мои 7 попыток ушли на пройдение 11-го теста.
Там можно без деления делать, только умножением... посчитаем вероятности для всех суффиксов и когда будет идти у нас будет вероятность для префикса и дальше пропихивается их произведение...
Ну я в итоге именно так и сдал :)
Какая-то не совсем div2 задача J. Как ее решать? Еще интересует решение D и G.
G — запихиваем листья (из которых ничего не выходит) и корни (в которые ничего не входит) в массив, сортируем по высоте, попарно соединяем
Как я понимаю, под div2 only обычно приносят скорее баянистые задачи, чем реально простые. Не знаю, что закодили ребята, которые эту задачу решили первыми, а у меня была стандартная, но довольно громоздкая (ещё и потребовавшая оптимизации) динамика за O(3^N * 2^N * logX): для каждой позиции (от больших к меньшим) в двоичной записи мы перебираем, в каких числах там будет 0, а в каких 1; для тех вариантов, где все ограничения [Li, Ri] удевлетворены, запоминаем какие из чисел уже можно продолжать по-любому (то есть что мы не припишем, они уже не выйдут за свой диапазон), а какие всё ещё могут оказаться меньше своего L или больше R, и вот тройка {номер бита, битмаска — какие из чисел ещё могут уйти ниже L, битмаска — какие из чисел ещё могут уйти выше R} будет наше состояние.
А можно пойти дальше и сделать рваный край по излому, тогда состояний будет logX * N * 2 * 3^N и переход за O(1)...
Ух ты :) То есть до N<=10 должно работать. Такое я бы наверное не решил.
А где-нибудь можно про "рваный край по излому" почитать?
Не знаю, не видел. Но это как рваный край... почти... в рваном хранится количество обработанных строк i и маска msk для следующей строки (условно так) и переход происходит перебором следующей маски. По излому мы также храним количество строк, которые уже полностью обработали i, потом храним количество элементов которое уже обработали в следующей строке j и саму маску msk, тогда переход будет просто перебрав значение в очередной клетке. Если двигаться по строкам, то это будет выглядеть как мы использвали i строк полностью и j элементов в следующей строки, а маска хранит информацию по каждому следующему элементу столбца...
Ок, понял, крутотень, спасибо :)
У нас вроде проще. Сначала формулой включений-исключений сводим к случаю L_i = 0. Теперь считаем одномерную динамику от префиксов всех R_i и x. Старшие биты все перебираем (2^8). Проверяем, что текущее значение старших битов нам подходит. Дальше смотрим, какие получились ограничения на префикс длиной на единицу меньше. Если там хотя бы одна максимальная степень двойки, то просто перемножаем все остальные ограничения — это ответ. Иначе берём значение уже посчитанной динамики. Получается O(4^N * N * log X).
Как А решалась?
Можно заметить, что четность количества инверсий (т.е. таких пар (i, j), что i < j и Ai > Aj) после каждого хода меняется. То есть достаточно посмотреть на четность инверсии в начальной последовательности и сравнить её с конечной... если равно тогда второй выигрывает, иначе выигрывает первый.
А можно отсортировать массив пузырьком и посчитать четность количества свопов элементов в процессе) Работает по той же самой причине