Магия питона или что за...

12 лет назад, # |

Может там сыграть на переполнении?

→ Ответить

yermak0v

12 лет назад, # ^ |

На питоне? Со встроенное длинкой? Или же длинка только для целых?

→ Ответить

12 лет назад, # ^ |

← Rev. 2 →

Я конечно кривой , но гугл не знает различий в питоне 2.7 и питоне 3 в выполнении sqrt. Я так понимаю что в направлении различия версий питона нужно покопать)

→ Ответить

Jarekczek

12 лет назад, # ^ |

← Rev. 2 →

На питоние 2.7 ответ такой же как на 3.1 (~~Посылки~~ мои посылки)

→ Ответить

ilyakor

12 лет назад, # ^ |

+21

< sarcasm> Ну да, ну да, "со встроенной длинкой". И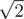 $\text{[math]}$ оно вам в длинке точно посчитает. И sin(1). < /sarcasm>

Не надо надеяться на магию, и надо понимать, как работает используемый вами инструмент. ИМХО, это большой минус языков вроде питона (точнее, даже не языка, а культуры, сложившейся вокруг него). Многие "программисты" полностью полагаются на магию, не понимая, как оно работает на самом деле.

→ Ответить

12 лет назад, # ^ |

← Rev. 3 →

меня при изучении питоне удивило что не могу найти за сколько работает какая-нибудь функция встроеная. Есть ли аналог сайту для с++. Конкретно интересует время выполнения.А то нет понимания как написаны функции питона и получается такой себе кот в мешке.

→ Ответить

ifsmirnov

12 лет назад, # ^ |

← Rev. 2 →

На официальном сайте есть.

Upd: извиняюсь, асимптотики алгоритмов там нет.

→ Ответить

Tinkturianec

12 лет назад, # ^ |

длинка только для целых. для вещественных в обеих версиях используется обычный сишный double, так что не очень понятно, для чего именно третий думаю, что и в корне различий не должно быть..

→ Ответить

vogel

12 лет назад, # |

В темах указан бинарный поиск по ответу. Вот и нужно думать в этом направлении.

→ Ответить

12 лет назад, # ^ |

← Rev. 5 →

Казалось бы, не очевидно почему бы этой штуке быть монотонной по x, если не понятно, когда это верно.

Поищите например минимальное неотрицательное целое такое, что x/2*2!=x таким спосоом (деление целочисленное)

→ Ответить

yermak0v

12 лет назад, # ^ |

А разве для целочисельного деления — ответ не 1? Или смысл в том, что бы найти его бинпоиском?

→ Ответить

12 лет назад, # ^ |

Смысл в том, что бинпоиском его нельзя искать по понятным причинам и прежде чем искать бинпоиском ответ на исх.задачу(как советовали) хорошо бы для начала понять почему бинпоиск будет работать.

→ Ответить

InvincibleUZ

12 лет назад, # ^ |

← Rev. 2 →

Она не монотонная. Для 5x10¹⁸ + 1 и 5x10¹⁸ - 1 ответ: !=, для 5x10¹⁸ ответ: ==

→ Ответить

NurlashKO

12 лет назад, # ^ |

-8

Magic : http://ideone.com/9tHg25

→ Ответить

12 лет назад, # |

Мне кажется, фича в том, что считается это в нецелых, которые вроде не длинка, а обычные даблы со всеми вытекающими ошибками. Например при i = int(1e230) уже даже нельзя вызвать math.sqrt(i*i)

→ Ответить

12 лет назад, # |

-19

Кто-то пробывал уже отослать с идеей переполнения?)

→ Ответить

InvincibleUZ

12 лет назад, # |

← Rev. 2 →

Долбил с другом эту задачу. Сдали. Прошла с первой попытки. В первой правке подсказка.

→ Ответить

12 лет назад, # |

← Rev. 2 →

-20

Мда уж. Задача простая же.

Подсказка в первой правке.

→ Ответить

12 лет назад, # ^ |

Может докажете почему это работает? Почему если для числа 100 все хорошо, то для числа 97 тоже?

→ Ответить

12 лет назад, # ^ |

Я не опирался на монотонность функции, или особенностях даблов. Просто искал верхнюю границу ответа while (math.sqrt (x * x) == x) x++. Где в виде x подставлял степени 10ки. Как только на 10 ^ 16 ответ нашелся быстро (10 ^ 16 + 1). Начал уменьшать старшие разряды, и просто брутфорсом проверял, быстро ли ответ найдется. То есть брал например 9 * 10 ^ 15, и увеличивал или уменьшал в зависимости от того, быстро нашелся ответ или нет. Я не знаю, как доказать это, скажем так, само как — то вышло :)

→ Ответить

12 лет назад, # ^ |

вот вы посмотрели, для 100 все хорошо, для 1000 все хорошо ... , плохо для 10^16+1, и начали искать на промежутке 10^15...10^16, так? А почему для числа 578 все верно?

→ Ответить

12 лет назад, # ^ |

Что вы имеете ввиду под 578? Я смотрел числа от 10 ^ 15 до 10 ^ 16, последовательно справа налево строя префикс числа, проверяя быстро ли находится ответ, где то по 1.5 — 2 секунды на каждое изменение числа, за это время мы пройдемся по внушительному количеству чисел с заданным префиксом, и поэтому интуитивно понимая, что число нужно брать больше.

→ Ответить

12 лет назад, # ^ |

578 — любое число, меньшее 10^15, не являющееся степенью десятки

→ Ответить