CodeChef invites you to participate in the May CookOff 2013 at http://www.codechef.com/COOK34.
Time: 19th May 2013 (2130 hrs) to 20th May 2013 (0000 hrs). (Indian Standard Time — +5:30 GMT) — Check your timezone.
Details: http://www.codechef.com/COOK34/
Registration: Just need to have a CodeChef user id to participate. New users please register here
Problem Setter: Abdullah Mahmud
Problem Tester: Shilp Gupta
Editorialist: Pradeep Mathias
It promises to deliver on an interesting set of algorithmic problems with something for all.
The contest is open for all and those, who are interested, are requested to have a CodeChef userid, in order to participate.











Расскажите, пожалуйста, как решается задачка про XOR.
И все-таки, как решается XOR Sum? Разбор этой задачи на сайте так и не появился.
Похоже разбор не хотят выкладывать.
Эта задача очень похожа на:
https://www.hackerrank.com/contests/codesprint4/challenges/stonegame
Я участвовал тогда в этом контесте и потратил несколько часов, чтоб решить ее (тупил :)).
Но сейчас я все быстро вспомнил и быстро сдал.
Решение такое.
Пусть a[1], ..., a[p] ≥ 2k, и a[j] < 2k при p < j ≤ n. То есть p чисел имеют старший бит 1. Положим для удобства a[j] = a[j] - 2k при 1 ≤ j ≤ p.
Если у b[1], ..., b[p] мы положим бит при 2k равным 1, то задача сведется к такой же задаче, но для чисел a[1], ..., a[p], a[p + 1], ..., a[n] и можно, например, рекурсивно вызвать функцию для этого массива (помним, что мы уже изменили исходный массив).
Иначе мы должны у чётного (ненулевого) количества чисел среди b[1], ..., b[p] положить бит при 2k равным 0, а для остальных положить его 1. Важно, что если какое-то из b[i] имеет бит при 2k равным 0, то можно выбрать остальные b[j] произвольными (с сохранением условия четности), а b[i] восстановить из условия на их XOR однозначно.
Пусть b[1], ..., b[i - 1] имеют бит при 2k равным 1, а b[i] имеет бит при 2k равным 0. Если все b[j] с нулевым битом при 2k — это b[j0 = i], b[j1], ..., b[jm], то количество способов вычисляется как
где c[j] = a[j] + 1. Дальше идет немного матана :)
Сумма всех таких произведений по наборам {j1, ..., jm} с нечётным m равна
Если раскрыть скобки в произведениях, то все станет понятно.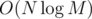 , где M = max a[i]. Я на контесте использовал сортировку вместо простого прохода для разделения чисел на меньшие 2k и остальные, поэтому решение было
, где M = max a[i]. Я на контесте использовал сортировку вместо простого прохода для разделения чисел на меньшие 2k и остальные, поэтому решение было  , но оно тоже прошло.
, но оно тоже прошло.
Теперь уже нетрудно найти сумму таких агрегатов по всем i за линейное время.
Надо просто предпросчитать префиксные и суффиксные произведения.
С учетом рекурсивнгого прохода по всем битам получается решение со сложностью
UPD
Наконец-то всё выглядит правильно после 100500 правок :)
UPD2
Понадобилась все-таки 100501 правка. Спасибо yarrr за личное сообщение.
Кто-нибудь умеет решать Rook Placement без OEIS?
Это какая-то чисто японская задача, трое японцев ее относительно рано и спокойно третьей сдавали.
Общее число таких последовательностей я честно угадал без OEIS в виде C(N+R-1,N) * C(N+C-1,N). При этом эта формула подсказала хорошое представление расстановки ладей, которое делает строки и столбцы независимыми. После этого для выигрышных позиций получилась dp-шка с формулой:
f(R,N) = f(R-1,N) + f(R,N-1),
то есть почти цешка, но с другой инициализацией. Здесь было понятно, что ответ можно вывести самому, но чтоб не терять время я все-таки сходил на OEIS :P
Если что, ответ на задачу — C(N+R-1,N) * C(N+C-1,N) — f(R,N) * f(C,N)).
Я выводил ответ следующим образом. Как уже заметили, строки и столбцы независимы, рассмотрим строки. Чтобы позиция была выигрышной необходимо и достаточно чтобы в любых первых К строках было не более К ладей, тогда можно сдвинуть ладьи на диагональ и получить допустимую комбинацию. Можно заметить что существует однозначное соответствие между такими расстановками ладей и скобочными последовательностями, а именно представим "(" как увеличение текущей строки на 1 и ")" как установку ладьи в текущую строку. Тогда мы хотим найти количество полу-правильных скобочных последовательностей (т.е. которые можно дополнить справа до правильной) состоящих из R "(" и N ")". Это можно вычислить аналогично одному из доказательств чисел Каталана путем отражения путей в табличке (http://en.wikipedia.org/wiki/Catalan_number#Second_proof). Тогда ответ для строк равен C(N+R,N) — C(N+R,N-1)
Окончательный ответ C(R+N-1,N)*C(C+N-1,C) — (C(N+R,N)-C(N+R,N-1))*(C(N+C,N)-C(N+C,N-1))